
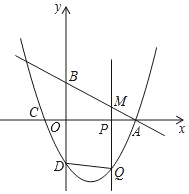
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
(1)求点A的坐标.
(2)求抛物线的表达式.
(3)当以B、D、Q,M为顶点的四边形是平行四边形时,求m的值.
【答案】(1)点A坐标为(4,0);(2)y=![]() x2﹣
x2﹣![]() x﹣2;(3)m=2或1+
x﹣2;(3)m=2或1+![]() 或1﹣
或1﹣![]() .
.
【解析】
(1)直线y=﹣![]() x+2中令y=0,即可求得A 点坐标;
x+2中令y=0,即可求得A 点坐标;
(2)将A、C坐标代入,利用待定系数法进行求解即可;
(3)先求出BD的长,用含m的式子表示出MQ的长,然后根据BD=QM,得到关于m的方程,求解即可得.
(1)令y=﹣![]() x+2=0,解得:x=4,
x+2=0,解得:x=4,
所以点A坐标为:(4,0);
(2)把点A、C坐标代入二次函数表达式,得
![]() ,
,
解得: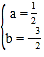 ,
,
故:二次函数表达式为:y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
(3)y=﹣![]() x+2中,令x=0,则y=2,故B(0,2),
x+2中,令x=0,则y=2,故B(0,2),
y=![]() x2﹣
x2﹣![]() x﹣2中,令x=0,则y=-2,故D(0,-2),
x﹣2中,令x=0,则y=-2,故D(0,-2),
所以BD=4,
设点M(m,﹣![]() m+2),则Q(m,
m+2),则Q(m,![]() m2﹣
m2﹣![]() m﹣2),
m﹣2),
则MQ=|(![]() m2﹣
m2﹣![]() m﹣2)-(﹣
m﹣2)-(﹣![]() m+2)|=|
m+2)|=|![]() m2﹣m﹣4|
m2﹣m﹣4|
以B、D、Q,M为顶点的四边形是平行四边形时,
则:|MQ|=BD=4,
即|![]() m2﹣m﹣4|=4,
m2﹣m﹣4|=4,
当![]() m2﹣m﹣4=-4时,
m2﹣m﹣4=-4时,
解得:m=2或m=0(舍去);
当![]() m2﹣m﹣4=4时,
m2﹣m﹣4=4时,
解得m=1±![]() ,
,
故:m=2或1+![]() 或1-
或1-![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】如图,扇形OAB中,∠AOB=60°,OA=4,点C为弧AB的中点,D为半径OA上一点,点A关于直线CD的对称点为E,若点E落在半径OA上,则OE=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王电子产品专柜以20元/副的价格批发了某新款耳机,在试销的60天内整理出了销售数据如下
销售数据(第x天) | 售价(元) | 日销售量(副) |
1≤x<35 | x+30 | 100﹣2x |
35≤x≤60 | 70 | 100﹣2x |
(1)若试销阶段每天的利润为W元,求出W与x的函数关系式;
(2)请问在试销阶段的哪一天销售利润W可以达到最大值?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
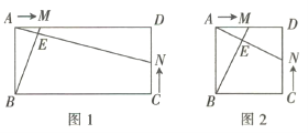
【题目】如图1,在矩形![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发向点
出发向点![]() 移动,速度为每秒1个单位长度,点
移动,速度为每秒1个单位长度,点![]() 从点
从点![]() 出发向点
出发向点![]() 移动,速度为每秒2个单位长度. 两点同时出发,且其中的任何一点到达终点后,另一点的移动同时停止.
移动,速度为每秒2个单位长度. 两点同时出发,且其中的任何一点到达终点后,另一点的移动同时停止.
(1)若两点的运动时间为![]() ,当
,当![]() 为何值时,
为何值时,![]() ?
?
(2)在(1)的情况下,猜想![]() 与
与![]() 的位置关系并证明你的结论.
的位置关系并证明你的结论.
(3)①如图2,当![]() 时,其他条件不变,若(2)中的结论仍成立,则
时,其他条件不变,若(2)中的结论仍成立,则![]() _________.
_________.
②当![]() ,
,![]() 时,其他条件不变,若(2)中的结论仍成立,则
时,其他条件不变,若(2)中的结论仍成立,则![]() _________(用含
_________(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
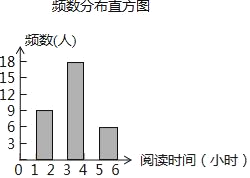
【题目】向阳中学为了解全校学生利用课外时间阅读的情况,调查者随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表(图).根据图表信息,解答下列问题:
频率分布表
阅读时间(小时) | 频数(人) | 频率 |
1≤x<2 | 9 | 0.15 |
2≤x<3 | a | m |
3≤x<4 | 18 | 0.3 |
4≤x<5 | 12 | n |
5≤x<6 | 6 | 0.1 |
合计 | b | 1 |
(1)填空:a= ,b= ,m= ,n= ;
(2)将频数分布直方图补充完整;
(3)阅读时间不低于5小时的6人中,有2名男生、4名女生.现从这6名学生中选取两名同学进行读书宣讲,求选取的两名学生恰好是两名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
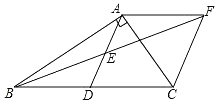
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:四边形ADCF是菱形;
(2)若AC=12,AB=16,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
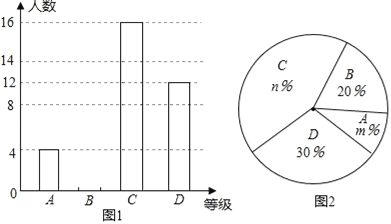
【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
(1)参加朗诵比赛的学生共有 人,并把条形统计图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形有圆心角为 度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() 点
点![]() 分别在边
分别在边![]() 上,
上,![]() 连接
连接![]() 点
点![]() 分别为
分别为![]() 的中点,则
的中点,则![]() 与
与![]() 的数量关系是: .
的数量关系是: .
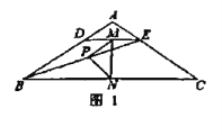
探究:把![]() 绕点
绕点![]() 顺时针方向旋转,如图
顺时针方向旋转,如图![]() ,连接
,连接![]()
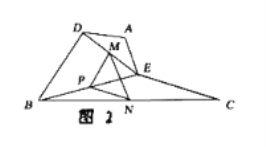
![]() 证明:
证明: ![]()
![]() 的度数为 _
的度数为 _![]()
应用:把![]() 绕点
绕点![]() 在平面内自由旋转,若
在平面内自由旋转,若![]() 面积的最大值为___________.
面积的最大值为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com