
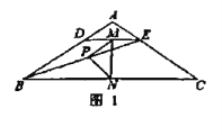
【题目】感知:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() 点
点![]() 分别在边
分别在边![]() 上,
上,![]() 连接
连接![]() 点
点![]() 分别为
分别为![]() 的中点,则
的中点,则![]() 与
与![]() 的数量关系是: .
的数量关系是: .
探究:把![]() 绕点
绕点![]() 顺时针方向旋转,如图
顺时针方向旋转,如图![]() ,连接
,连接![]()
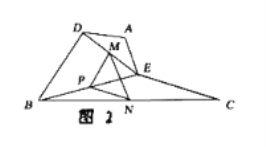
![]() 证明:
证明: ![]()
![]() 的度数为 _
的度数为 _![]()
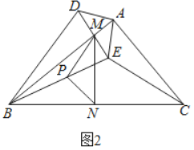
应用:把![]() 绕点
绕点![]() 在平面内自由旋转,若
在平面内自由旋转,若![]() 面积的最大值为___________.
面积的最大值为___________.
【答案】感知:![]() ;探究:
;探究:![]() 详见解析;
详见解析;![]() ;
; ![]()
【解析】
感知:由题意可得BD=CE,由三角形中位线可得BD=2PM,CE=2PN,可得PM=PN;
探究:(1)由“SAS”可证![]() ,由三角形中位线定理可得BD=2PM,CE=2PN,可得PM=PN;
,由三角形中位线定理可得BD=2PM,CE=2PN,可得PM=PN;
(2)由全等三角形的性质可得∠ABD=∠ACE,由平行线的性质可得∠BDE=∠MPE,∠BNP=∠BCE,由三角形外角性质可求∠MPN=60°,可证△PMN是等边三角形,即可求解;
应用:先判断出BD最大时,△PMN的面积最大,而BD最大值是AB+AD=12,即可求解.
解:感知:∵AB=AC,AD=AE
∴BD=CE
∴ BD=2PM,CE=2PN
∴PM=PN
故答案为PM=PN.
探究:
![]() 证明:
证明:![]()
![]()
又![]() .
.
![]() (SAS).
(SAS).
![]() .
.
![]() 点
点![]() 分别是
分别是![]() 的中点,
的中点,
![]()
![]() 点
点![]() 分别是
分别是![]() 的中点
的中点
![]() .
.
![]()
(2)∵![]()
∴∠ABD=∠ACE
∵PM=PN
∴△PMN是等腰三角形
∵PM∥BD
∴∠DBE=∠MPE
∵PN∥BD
∴∠BNP=∠BCE
∵∠DBN=∠DBP+∠EBC=∠MPE+∠EBC
∴∠MPN=∠MPE+∠EPN=∠MPE+∠EBC+∠PNB=∠DBN+∠BCE=∠ABC+∠ABD+∠BCE=∠ABC+∠ACE+∠BCE=∠ABC+∠ACB
∴∠BAC=120°
∴∠ACB+∠ABC=60°
∴∠MPN=60°
∴△PMN是等边三角形
∴∠PMN=60°
故答案为60°.
(3)由(2)知△PMN是等边三角形,PM=PN=![]() BD
BD
∴PM最大时,△PMN面积最大,PM最小时,△PMN面积最小
∴点D在BA的延长线上,△PMN的面积最大
∴BD=AB+AD=12
∴PM=6
∴![]()
故答案为![]() .
.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
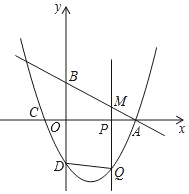
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
(1)求点A的坐标.
(2)求抛物线的表达式.
(3)当以B、D、Q,M为顶点的四边形是平行四边形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】奇异果是新西兰的特产,其实它的祖籍在中国,又名“猕猴桃”.2018年1月份至6月份我市某大型超市新西兰品种的奇异果销售价格y(元/盒)与月份x(1≤x≤6,且x为整数)之间的函数关系如下表:

7月份至12月份奇异果的销售价格y(元/盒)与月份x之间满足函数关系式:y=2x+20(7≤x≤12且x为整数).该超市去年奇异果销售数量z(盒)与月份x(1≤x≤12,且x为整数)之间存在如图所示的变化趋势.若去年该超市奇异果的进价为每盒20元,销售奇异果需要一名超市员工,该员工每月固定人工费用为1500元.
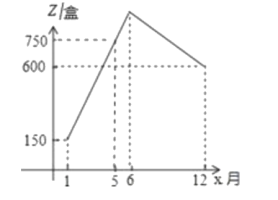
(1)请观察图表中的数据信息直接写出2018年1月份至6月份销售价格y与x之间的函数关系式__ ,根据如图所示的变化趋势,直接写出去年每月销售数量z与x之间满足的函数关系式__ .
(2)求出去年每月该超市的利润w(元)与月份x之间满足的函数关系式.(利润=收入成本费用)
(3)从今年1月份开始,超市决定每卖出一盒奇异果,公司向希望工程捐款2元,奇异果的进价为每盒26元,虽然今年1月份奇异果的销售价格比去年12月份增加4元,但1月份销售数量仍比去年12月份增加了0.4a%;2月份销售价格在1月份的基础上增加了0.5a%,由于其它水果陆续上市,2月份的销售量与1月份持平,这样2月份的利润达到了15780元,请参考以下数据,求出整数a的值.(参考数据:![]() =2025,
=2025,![]() =2116,
=2116,![]() =2209)
=2209)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的道路AB上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,假设他们分别以不同的速度匀速行驶,甲先出发6分钟后,乙才出发,乙的速度为![]() 千米/分,在整个过程中,甲、乙两人之间的距离y(千米)与甲出发的时间x(分)之间的部分函数图象如图.
千米/分,在整个过程中,甲、乙两人之间的距离y(千米)与甲出发的时间x(分)之间的部分函数图象如图.
(1)A、B两地相距____千米,甲的速度为____千米/分;
(2)求线段EF所表示的y与x之间的函数表达式;
(3)当乙到达终点A时,甲还需多少分钟到达终点B?

查看答案和解析>>
科目:初中数学 来源: 题型:
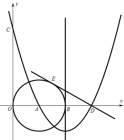
【题目】如图,已知点![]() ,以
,以![]() 为圆心作
为圆心作![]() 与
与![]() 轴切于原点,与
轴切于原点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,过
,过![]() 作
作![]() 的切线
的切线![]() .
.
(1)以直线![]() 为对称轴的抛物线过点
为对称轴的抛物线过点![]() 及点
及点![]() ,求次抛物线的解析式;
,求次抛物线的解析式;
(2)第(1)问中的抛物线与![]() 轴的另一个交点为
轴的另一个交点为![]() ,过
,过![]() 作
作![]() 的切线
的切线![]() ,
,![]() 为切点,求此切线长;
为切点,求此切线长;
(3)点![]() 是切线DE上的一个动点,当
是切线DE上的一个动点,当![]() 与
与![]() 相似时,求出点
相似时,求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价(元/件) | 40 | 90 |
售价(元/件) | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
(Ⅰ)写出y关于x的函数关系式;
(Ⅱ)该商场计划最多投入8000元用于购买这两种商品,
①至少要购进多少件甲商品?
②若销售完这些商品,则商场可获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
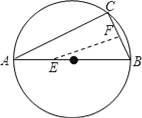
【题目】如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着ABA方向运动,设运动时间为t(s)(0≤t<3),连接EF,当t为_____s时,△BEF是直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com