
【题目】甲、乙两人在笔直的道路AB上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,假设他们分别以不同的速度匀速行驶,甲先出发6分钟后,乙才出发,乙的速度为![]() 千米/分,在整个过程中,甲、乙两人之间的距离y(千米)与甲出发的时间x(分)之间的部分函数图象如图.
千米/分,在整个过程中,甲、乙两人之间的距离y(千米)与甲出发的时间x(分)之间的部分函数图象如图.
(1)A、B两地相距____千米,甲的速度为____千米/分;
(2)求线段EF所表示的y与x之间的函数表达式;
(3)当乙到达终点A时,甲还需多少分钟到达终点B?

【答案】(1)24,![]() ;(2)y=﹣
;(2)y=﹣![]() x+33;(3)当乙到达终点A时,甲还需50分钟到达终点B.
x+33;(3)当乙到达终点A时,甲还需50分钟到达终点B.
【解析】
(1)观察图象知A、B两地相距为24km,由纵坐标看出甲先行驶了2千米,由横坐标看出甲行驶2千米用了6分钟,则甲的速度是![]() 千米/分钟;
千米/分钟;
(2)列方程求出相遇时的时间,求出点F的坐标,再运用待定系数法解答即可;
(3)根据相遇前甲行驶的路程除以乙行驶的速度,可得乙到达A站需要的时间,根据相遇前乙行驶的路程除以甲行驶的速度,可得甲到达B站需要的时间,再根据有理数的减法,可得答案
解:(1)观察图象知A、B两地相距为24km,
∵甲先行驶了2千米,由横坐标看出甲行驶2千米用了6分钟,
∴甲的速度是![]() 千米/分钟;
千米/分钟;
故答案为:24,![]() ;
;
(2)设甲乙经过a分钟相遇,根据题意得,
![]() ,解答a=18,
,解答a=18,
∴F(18,0),
设线段EF表示的y与x之间的函数表达式为y=kx+b,根据题意得,
![]() ,解得
,解得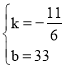 ,
,
∴线段EF表示的y与x之间的函数表达式为y=﹣![]() x+33;
x+33;
(3)相遇后乙到达A地还需:(18×![]() )÷
)÷![]() =4(分钟),
=4(分钟),
相遇后甲到达B站还需:(12×![]() )÷
)÷![]() =54(分钟)
=54(分钟)
当乙到达终点A时,甲还需54﹣4=50分钟到达终点B.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数图象的对称轴为直线x=2,顶点为点C,直线y=x+m与该二次函数的图象交于点A,B两点,其中点A的坐标为(5,8),点B在y轴上.
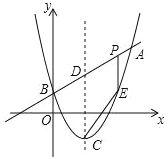
(1)求m的值和该二次函数的表达式.为线段AB上一个动点(点P不与A,B两点重合),过点P作x轴的垂线,与这个二次函数的图象交于点E.
①设线段PE的长为h,求h与x之间的函数关系式,并写出自变量x的取值范围.
②若直线AB与这个二次函数图象的对称轴的交点为D,求当四边形DCEP是平行四边形时点P的坐标.
(3)若点P(x,y)为直线AB上的一个动点,试探究:以PB为直径的圆能否与坐标轴相切?如果能请求出点P的坐标,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
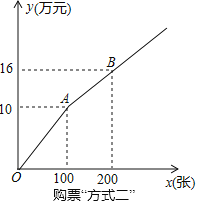
【题目】世界500强H公司决定购买某演唱会门票奖励部分优秀员工,演唱会的购票方式有以下两种,
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元(其中总费用=广告赞助费+门票费);
方式二:如图所示,设购买门票x张,总费用为y万元
(1)求用购票“方式一”时y与x的函数关系式;
(2)若H、A两家公司分别釆用方式一、方式二购买本场演唱会门票共400张,且A公司购买超过100张,两公司共花费27.2万元,求H、A两公司各购买门票多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,按如下步骤作图:①以点A为圆心,AB长为半径画弧;②以点C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD.
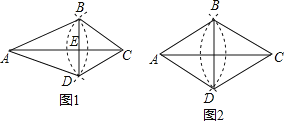
(1)填空:△ABC≌△ ;AC和BD的位置关系是
(2)如图2,当AB=BC时,猜想四边形ABCD是什么四边形,并证明你的结论.
(3)在(2)的条件下,若AC=8cm,BD=6cm,则点B到AD的距离是 cm,若将四边形ABCD通过割补,拼成一个正方形,那么这个正方形的边长为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】25 日某路段雷达测速区监测到一组汽车时速数据,经整理得到如下频数表和频数直方图(每组含后一边界值,不含前一边界值).
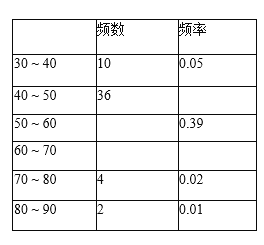
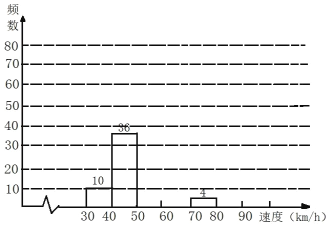
(1)请你把表中的数据填写完整.
(2)补全频数直方图.
(3)若该路段限速 70(汽车时速高于 70 千米/小时即为违章),抽测到违章车辆有多少辆?统计表明 25 日全天通过这个路段的汽车大约有 15000 辆,请估计这天超速违章的车辆有多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂计划每天生产零件![]() 个,但实际每天生产量与计划量相比有出入. 下表是某周的生产情况(超产数量记为正、减产数量记为负):
个,但实际每天生产量与计划量相比有出入. 下表是某周的生产情况(超产数量记为正、减产数量记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)由表可知该厂星期四生产零件 个,这周实际生产零件 个.(用含![]() 的代数式表示)
的代数式表示)
(2) 产量最高日比最低日多生产零件 个.
(3) 若该周厂计划每天生产零件数是![]() ,每个零件应支付工资
,每个零件应支付工资![]() 元,且每天超计划数的零件每个另奖
元,且每天超计划数的零件每个另奖![]() 元,那这周实际应支付工资多少元?
元,那这周实际应支付工资多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
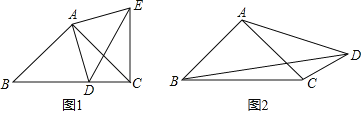
【题目】(1)如图1,在Rt△ABC和Rt△ADE中,AB=AC,AD=AE,且点D在BC边上滑动(点D不与点B,C重合),连接EC,
①则线段BC,DC,EC之间满足的等量关系式为 ;
②求证:BD2+CD2=2AD2;
(2)如图2,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=9,CD=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商人小周于上周买进某农场品10000![]() ,每千克2.4元,进入批发市场后共占5个摊位,每个摊位最多能容纳2000
,每千克2.4元,进入批发市场后共占5个摊位,每个摊位最多能容纳2000![]() 该品种的农产品,每个摊位的市场管理价为每天20元.下表为本周内该农产品每天的批发价格比前一天的涨跌情况.
该品种的农产品,每个摊位的市场管理价为每天20元.下表为本周内该农产品每天的批发价格比前一天的涨跌情况.
星期 | 一 | 二 | 三 | 四 | 五 |
与前一天相比价格的涨跌情况/元 | +0.3 | -0.1 | +0.25 | +0.2 | -0.5 |
当天的交易量/ | 2500 | 2000 | 3000 | 1500 | 1000 |
(1)星期四该农产品的价格为每千克多少元?
(2)本周内该农产品的最高价格为每千克多少元?最低价格为每千克多少元?
(3)小周在销售过程中采用逐步减少摊位个数的方法来降低成本,增加收益,这样他在本周的买卖中共赚了多少钱?请你帮他算一算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com