
【题目】商人小周于上周买进某农场品10000![]() ,每千克2.4元,进入批发市场后共占5个摊位,每个摊位最多能容纳2000
,每千克2.4元,进入批发市场后共占5个摊位,每个摊位最多能容纳2000![]() 该品种的农产品,每个摊位的市场管理价为每天20元.下表为本周内该农产品每天的批发价格比前一天的涨跌情况.
该品种的农产品,每个摊位的市场管理价为每天20元.下表为本周内该农产品每天的批发价格比前一天的涨跌情况.
星期 | 一 | 二 | 三 | 四 | 五 |
与前一天相比价格的涨跌情况/元 | +0.3 | -0.1 | +0.25 | +0.2 | -0.5 |
当天的交易量/ | 2500 | 2000 | 3000 | 1500 | 1000 |
(1)星期四该农产品的价格为每千克多少元?
(2)本周内该农产品的最高价格为每千克多少元?最低价格为每千克多少元?
(3)小周在销售过程中采用逐步减少摊位个数的方法来降低成本,增加收益,这样他在本周的买卖中共赚了多少钱?请你帮他算一算.
【答案】(1)星期四该农产品的价格为每千克3.05元;(2)最高价格为每千克3.05元,最低价格为每千克2.55元;(3)共赚了3325元
【解析】
(1)根据价格的涨跌情况即可作出判断;
(2)计算出每天的价格即可作出判断;
(3)根据涨跌×交易量-摊位费用=收益,即可进行计算.
解:(1)2.4+0.3-0.1+0.25+0.2
=3.05元
答:星期四该农产品的价格为每千克3.05元
(2)星期一:2.4+0.3=2.7元
星期二:2.4+0.3-0.1=2.6元
星期三:2.4+0.3-0.1+0.25=2.85元
星期四:2.4+0.3-0.1+0.25+0.2=3.05元
星期五:2.4+0.3-0.1+0.25+0.2-0.5=2.55元
答:最高价格为每千克3.05元,最低价格为每千克2.55元.
(3)2500×0.3+2000×(0.3-0.1)+3000×(0.3-0.1+0.25)+1500×(0.3-0.1+0.25+0.2)+1000×(0.3-0.1+0.25+0.2-0.5)-5×20-4×20-3×20-2×20-1×20
=750+400+1350+975+150-100-80-60-40-20
=3325元
答:共赚了3325元


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的道路AB上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,假设他们分别以不同的速度匀速行驶,甲先出发6分钟后,乙才出发,乙的速度为![]() 千米/分,在整个过程中,甲、乙两人之间的距离y(千米)与甲出发的时间x(分)之间的部分函数图象如图.
千米/分,在整个过程中,甲、乙两人之间的距离y(千米)与甲出发的时间x(分)之间的部分函数图象如图.
(1)A、B两地相距____千米,甲的速度为____千米/分;
(2)求线段EF所表示的y与x之间的函数表达式;
(3)当乙到达终点A时,甲还需多少分钟到达终点B?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐数量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A,B,C,D,E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
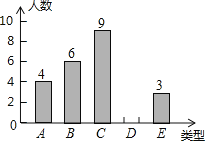
(1)补全条形统计图;
(2)这30名职工捐书本数的众数是 本,中位数是 本;
(3)求这30名职工捐书本数的平均数是多少本?并估计该单位750名职工共捐书多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
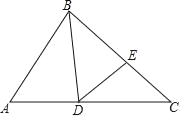
【题目】如图,BD是△ABC的角平分线,点E位于边BC上,已知BD是BA与BE的比例中项.
(1)求证:∠CDE=![]() ∠ABC;
∠ABC;
(2)求证:ADCD=ABCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOD=90°,OC平分∠BOD,∠AOB与∠BOC的度数的比是4︰7
(1)求∠AOB的度数.
(2)若以点O为观察中心,以OD为正北方向,则从方位角来说,射线OC在什么方向?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,若AB=6,BC=4![]() ,则FD=__________.
,则FD=__________.
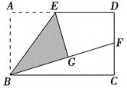
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 内部有若干个点,用这些点以及正方形
内部有若干个点,用这些点以及正方形![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 、
、![]() 把原正方形分割成一些三角形(互相不重叠)
把原正方形分割成一些三角形(互相不重叠)
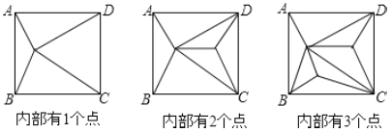
(1)填写下表:
正方形 | 1 | 2 | 3 | 4 | … |
|
分割成的三角形的个数 | 4 | 6 | ______ | ______ | … | ______ |
(2)如果原正方形内有101个点,此时原正方形被分割成多少个三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作已知角的角平分线”的尺规作图过程.
已知:如图1,∠MON.
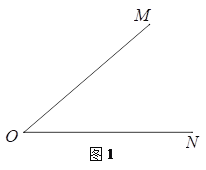
求作:射线OP,使它平分∠MON.
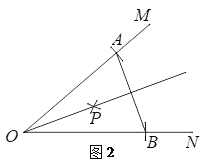
作法:如图2,
(1)以点O为圆心,任意长为半径作弧,交OM于点A,交ON于点B;
(2)连结AB;
(3)分别以点A,B为圆心,大于![]() AB的长为半径作弧,两弧相交于点P;
AB的长为半径作弧,两弧相交于点P;
(4)作射线OP.
所以,射线OP即为所求作的射线.
请回答:该尺规作图的依据是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用粗线在数轴上表示了一个“范围”,这个“范围”包含所有大于1且小于2的数(数轴上1与2这两个数的点空心,表示这个范围不包含数1和2).
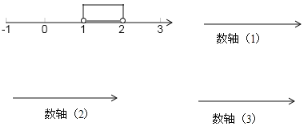
请你在数轴上表示出一个范围,使得这个范围:
(1)包含所有大于-3且小于0的数[画在数轴(1)上];
(2)包含![]() 这两个数,且只含有5个整数[画在数轴(2)上];
这两个数,且只含有5个整数[画在数轴(2)上];
(3)同时满足以下三个条件:[画在数轴(3)上]
①至少有100对互为相反数和100对互为倒数;
②有最小的正整数;
③这个范围内最大的数与最小的数表示的点的距离大于3但小于4.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com