
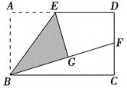
【题目】如图,在矩形ABCD中,点E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,若AB=6,BC=4![]() ,则FD=__________.
,则FD=__________.
【答案】4
【解析】
根据点E是AD的中点以及翻折的性质可以求出AE=DE=EG,然后利用“HL”证明△EDF和△EGF全等,根据全等三角形对应边相等可证得DF=GF;设FD=x,表示出FC、BF,然后在Rt△BCF中,利用勾股定理列式进行计算即可.
∵E是AD的中点,
∴AE=DE,
∵△ABE沿BE折叠后得到△GBE,
∴AE=EG,AB=BG,
∴ED=EG,
∵在矩形ABCD中,
∴∠A=∠D=90°,
∴∠EGF=90°,
在Rt△EDF和Rt△EGF中,
![]() ,
,
∴Rt△EDF≌Rt△EGF(HL),
∴DF=FG,
设DF=x,则BF=6+x,CF=6-x,
在Rt△BCF中,(4![]() )2+(6-x)2=(6+x)2,
)2+(6-x)2=(6+x)2,
解得x=4.
故答案为:4.


科目:初中数学 来源: 题型:
【题目】25 日某路段雷达测速区监测到一组汽车时速数据,经整理得到如下频数表和频数直方图(每组含后一边界值,不含前一边界值).
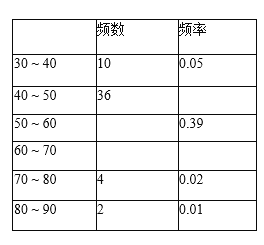
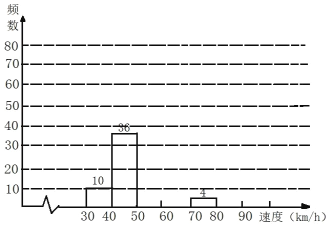
(1)请你把表中的数据填写完整.
(2)补全频数直方图.
(3)若该路段限速 70(汽车时速高于 70 千米/小时即为违章),抽测到违章车辆有多少辆?统计表明 25 日全天通过这个路段的汽车大约有 15000 辆,请估计这天超速违章的车辆有多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义:若∠α的度数是∠β的度数的n倍,则∠α叫做∠β的n倍角.
(1)若∠M=10°21′,请直接写出∠M的3倍角的度数;
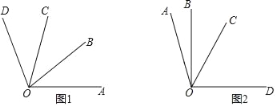
(2)如图1,若∠AOB=∠BOC=∠COD,请直接写出图中∠AOB的所有2倍角;
(3)如图2,若∠AOC是∠AOB的3倍角,∠COD是∠AOB的4倍角,且∠BOD=90°,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD,点E在边AB上,M、N分别在射线BC和射线AD上,连接EM,EN,将三角形MBE沿EM折叠(把物体的一部分翻转和另一部分贴拢),点B落在点B’处;将三角形NAE沿EN折叠,点A落在点A’处.
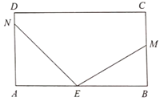
(1)若![]() ,
,![]() ,用直尺、量角器画出射线EB’与EA’;
,用直尺、量角器画出射线EB’与EA’;
(2)若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() ,
,![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商人小周于上周买进某农场品10000![]() ,每千克2.4元,进入批发市场后共占5个摊位,每个摊位最多能容纳2000
,每千克2.4元,进入批发市场后共占5个摊位,每个摊位最多能容纳2000![]() 该品种的农产品,每个摊位的市场管理价为每天20元.下表为本周内该农产品每天的批发价格比前一天的涨跌情况.
该品种的农产品,每个摊位的市场管理价为每天20元.下表为本周内该农产品每天的批发价格比前一天的涨跌情况.
星期 | 一 | 二 | 三 | 四 | 五 |
与前一天相比价格的涨跌情况/元 | +0.3 | -0.1 | +0.25 | +0.2 | -0.5 |
当天的交易量/ | 2500 | 2000 | 3000 | 1500 | 1000 |
(1)星期四该农产品的价格为每千克多少元?
(2)本周内该农产品的最高价格为每千克多少元?最低价格为每千克多少元?
(3)小周在销售过程中采用逐步减少摊位个数的方法来降低成本,增加收益,这样他在本周的买卖中共赚了多少钱?请你帮他算一算.
查看答案和解析>>
科目:初中数学 来源: 题型:
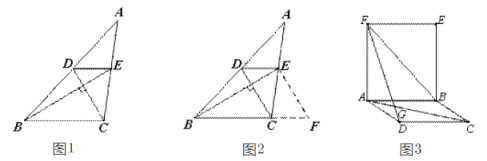
【题目】阅读下面的材料:小锤遇到一个问题:如图①,在△ABC中,DE//BC分别交AB于点D,交AC于点E,已知CD![]() BE,CD=2,BE=3,求BC+DE的值.
BE,CD=2,BE=3,求BC+DE的值.
小锤发现,过点E作EF![]() DC,交BC的延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决.
DC,交BC的延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决.
(1)请按照上述思路完成小锤遇到的问题;
(2)参考小锤思考问题的方法,解决下面的问题:如图②,四边形ABCD是平行四边形,四边形ABEF是矩形,AC与DF交于点G,AC=BF=DF,求∠DGC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
(1)求抛物线的解析式;
(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,![]() ,
,![]() .将矩形ABCD沿过点C的直线折叠,使点B落在对角线AC上的点E处,折痕交AB于点F.
.将矩形ABCD沿过点C的直线折叠,使点B落在对角线AC上的点E处,折痕交AB于点F.
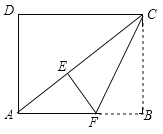
(1)求线段AC的长.
(2)求线段EF的长.
(3)点G在线段CF上,在边CD上存在点H,使以E、F、G、H为顶点的四边形是平行四边形,请画出![]() ,并直接写出线段DH的长.
,并直接写出线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上![]() 两点相距
两点相距![]() 个单位长度,机器人从
个单位长度,机器人从![]() 点出发去
点出发去![]() 点,
点,![]() 点在
点在![]() 点右侧.规定向右为前进,第一次它前进
点右侧.规定向右为前进,第一次它前进![]() 个单位长度,第二次它后退
个单位长度,第二次它后退![]() 个单位长度,第三次再前进
个单位长度,第三次再前进![]() 个单位长度,第四次又后退
个单位长度,第四次又后退![]() 个单位长度……按此规律行进,如果
个单位长度……按此规律行进,如果![]() 点在数轴上表示的数为
点在数轴上表示的数为![]() ,那么
,那么
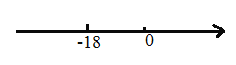
(1)求出![]() 点在数轴上表示的数.
点在数轴上表示的数.
(2)经过第七次行进后机器人到达点![]() ,第八次行进后到达点
,第八次行进后到达点![]() ,点
,点![]() 到
到![]() 点的距离相等吗?请说明理由.
点的距离相等吗?请说明理由.
(3)机器人在未到达![]() 点之前,经过
点之前,经过![]() 次(
次(![]() 为正整数)行进后,它在数轴上表示的数应如何用含
为正整数)行进后,它在数轴上表示的数应如何用含![]() 的代数式表示?
的代数式表示?
(4)如果![]() 点在原点的右侧,那么机器人经过
点在原点的右侧,那么机器人经过![]() 次行进后,它在
次行进后,它在![]() 点的什么位置?请通过计算说明.
点的什么位置?请通过计算说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com