
【题目】已知数轴上![]() 两点相距
两点相距![]() 个单位长度,机器人从
个单位长度,机器人从![]() 点出发去
点出发去![]() 点,
点,![]() 点在
点在![]() 点右侧.规定向右为前进,第一次它前进
点右侧.规定向右为前进,第一次它前进![]() 个单位长度,第二次它后退
个单位长度,第二次它后退![]() 个单位长度,第三次再前进
个单位长度,第三次再前进![]() 个单位长度,第四次又后退
个单位长度,第四次又后退![]() 个单位长度……按此规律行进,如果
个单位长度……按此规律行进,如果![]() 点在数轴上表示的数为
点在数轴上表示的数为![]() ,那么
,那么
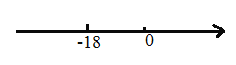
(1)求出![]() 点在数轴上表示的数.
点在数轴上表示的数.
(2)经过第七次行进后机器人到达点![]() ,第八次行进后到达点
,第八次行进后到达点![]() ,点
,点![]() 到
到![]() 点的距离相等吗?请说明理由.
点的距离相等吗?请说明理由.
(3)机器人在未到达![]() 点之前,经过
点之前,经过![]() 次(
次(![]() 为正整数)行进后,它在数轴上表示的数应如何用含
为正整数)行进后,它在数轴上表示的数应如何用含![]() 的代数式表示?
的代数式表示?
(4)如果![]() 点在原点的右侧,那么机器人经过
点在原点的右侧,那么机器人经过![]() 次行进后,它在
次行进后,它在![]() 点的什么位置?请通过计算说明.
点的什么位置?请通过计算说明.
【答案】(1)52;(2)点![]() 到
到![]() 点的距离相等;(3)
点的距离相等;(3)![]() 或
或![]() ;(4)
;(4)![]() 点左边
点左边![]() 个单位长度处.
个单位长度处.
【解析】
(1)根据数轴上两点之间的距离,进行计算求解;(2)根据题意分别表示出M,N所表示的数,然后根据两点间距离公式计算MA,NA的长度,从而求解;(3)分n为奇数或偶数,两种情况,根据题意列式求解;(4)将n=99代入,求值计算即可.
解:(1)由题意得![]() ,
,
![]() 点在数轴上表示的数为
点在数轴上表示的数为![]() .
.
(2)点![]() 在数轴上表示的数为
在数轴上表示的数为![]()
![]() ,
,
点![]() 在数轴上表示的数为
在数轴上表示的数为![]()
![]()
MA=-14-(-18)=4;NA=-18-(-22)=4
∴点![]() 到
到![]() 点的距离相等
点的距离相等
(3)当![]() 为奇数时,它在数轴上表示的数为:
为奇数时,它在数轴上表示的数为:
![]()
![]() .
.
当![]() 为偶数时,它在数轴上表示的数为:
为偶数时,它在数轴上表示的数为:
![]()
![]() .
.
(4)当n=99时,![]()
52-32=20
答:机器人经过![]() 次行进后,它在
次行进后,它在![]() 点的左边
点的左边![]() 个单位长度处.
个单位长度处.


科目:初中数学 来源: 题型:
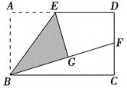
【题目】如图,在矩形ABCD中,点E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,若AB=6,BC=4![]() ,则FD=__________.
,则FD=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
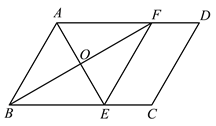
【题目】如图,在□ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形;
(2)连接CF,若∠ABC=60°,AB= 4,AF =2DF,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上A. B两点对应的数分别为4和2,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A.点B的距离相等,写出点P对应的数;
(2)数轴上是否存在点P,使点P到点A. 点B的距离之和为10?若存在,求出x的值;若不存在,请说明理由;
(3)若点A点B和点P(点P在原点)同时向右运动,它们的速度分别为2、1、1个长度单位/分,问:多少分钟后P点到点A点B的距离相等?(直接写出结果)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用粗线在数轴上表示了一个“范围”,这个“范围”包含所有大于1且小于2的数(数轴上1与2这两个数的点空心,表示这个范围不包含数1和2).
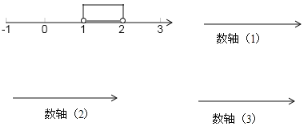
请你在数轴上表示出一个范围,使得这个范围:
(1)包含所有大于-3且小于0的数[画在数轴(1)上];
(2)包含![]() 这两个数,且只含有5个整数[画在数轴(2)上];
这两个数,且只含有5个整数[画在数轴(2)上];
(3)同时满足以下三个条件:[画在数轴(3)上]
①至少有100对互为相反数和100对互为倒数;
②有最小的正整数;
③这个范围内最大的数与最小的数表示的点的距离大于3但小于4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店准备购进甲、乙两种图书共100本,购书款不高于2224元,预这100本图书全部售完的利润不低于1100元,两种图书的进价、售价如表所示:
甲种图书 | 乙种图书 | |
进价(元/本) | 16 | 28 |
售价(元/本) | 26 | 40 |
请回答下列问题:
(1)书店有多少种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?(请你用所学的函数知识来解决)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只甲虫在5![]() 5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为:
5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为:![]() (+1,+3);从C到D 记为:
(+1,+3);从C到D 记为:![]() (+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.
(+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.
(1)填空:![]() 记为( , ),
记为( , ), ![]() 记为( , );
记为( , );
(2)若甲虫的行走路线为:![]() ,请你计算甲虫走过的路程.
,请你计算甲虫走过的路程.
(3)若这只甲虫去Q的行走路线依次为:A→M(+2,+2),M→N(+2,-1),N→P(-2,+3),P→Q(-1,-2),请依次在图2标出点M、N、P、Q的位置.
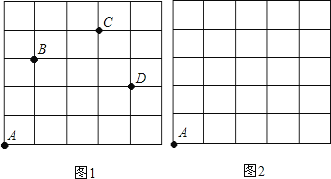
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2,在第四组内的两名选手记为:B1、B2,从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com