
【题目】如图,用粗线在数轴上表示了一个“范围”,这个“范围”包含所有大于1且小于2的数(数轴上1与2这两个数的点空心,表示这个范围不包含数1和2).
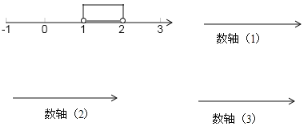
请你在数轴上表示出一个范围,使得这个范围:
(1)包含所有大于-3且小于0的数[画在数轴(1)上];
(2)包含![]() 这两个数,且只含有5个整数[画在数轴(2)上];
这两个数,且只含有5个整数[画在数轴(2)上];
(3)同时满足以下三个条件:[画在数轴(3)上]
①至少有100对互为相反数和100对互为倒数;
②有最小的正整数;
③这个范围内最大的数与最小的数表示的点的距离大于3但小于4.
科目:初中数学 来源: 题型:
【题目】商人小周于上周买进某农场品10000![]() ,每千克2.4元,进入批发市场后共占5个摊位,每个摊位最多能容纳2000
,每千克2.4元,进入批发市场后共占5个摊位,每个摊位最多能容纳2000![]() 该品种的农产品,每个摊位的市场管理价为每天20元.下表为本周内该农产品每天的批发价格比前一天的涨跌情况.
该品种的农产品,每个摊位的市场管理价为每天20元.下表为本周内该农产品每天的批发价格比前一天的涨跌情况.
星期 | 一 | 二 | 三 | 四 | 五 |
与前一天相比价格的涨跌情况/元 | +0.3 | -0.1 | +0.25 | +0.2 | -0.5 |
当天的交易量/ | 2500 | 2000 | 3000 | 1500 | 1000 |
(1)星期四该农产品的价格为每千克多少元?
(2)本周内该农产品的最高价格为每千克多少元?最低价格为每千克多少元?
(3)小周在销售过程中采用逐步减少摊位个数的方法来降低成本,增加收益,这样他在本周的买卖中共赚了多少钱?请你帮他算一算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是( )
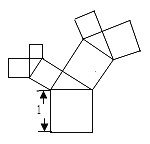
A.1B.2018C.2019D.2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个口袋中有4个完全相同的小球,把它们分别标号1、2、3、4.小明先随机地摸出一个小球,小强再随机地摸出一个小球.记小明摸出球的标号为x,小强摸出的球标号为y.小明和小强在此基础上共同协商一个游戏规则:当x>y时小明获胜。否则小强获胜.
(1)若小明摸出的球不放回,求小明获胜的概率;
(2)若小明摸出的球放回后小强再随机摸球,问他们制定的游戏规则公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
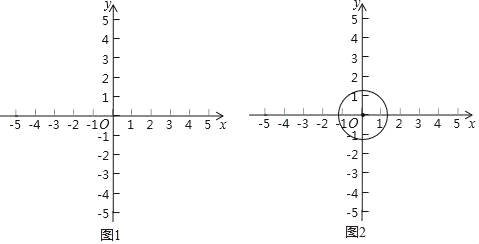
【题目】在平面直角坐标系xOy中,点M的坐标为(x1,y1),点N的坐标为(x2,y2),且x1≠x2,y1≠y2,以MN为边构造菱形,若该菱形的两条对角线分别平行于x轴,y轴,则称该菱形为边的“坐标菱形”.
(1)已知点A(2,0),B(0,2![]() ),则以AB为边的“坐标菱形”的最小内角为 ;
),则以AB为边的“坐标菱形”的最小内角为 ;
(2)若点C(1,2),点D在直线y=5上,以CD为边的“坐标菱形”为正方形,求直线CD 表达式;
(3)⊙O的半径为![]() ,点P的坐标为(3,m).若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
,点P的坐标为(3,m).若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上![]() 两点相距
两点相距![]() 个单位长度,机器人从
个单位长度,机器人从![]() 点出发去
点出发去![]() 点,
点,![]() 点在
点在![]() 点右侧.规定向右为前进,第一次它前进
点右侧.规定向右为前进,第一次它前进![]() 个单位长度,第二次它后退
个单位长度,第二次它后退![]() 个单位长度,第三次再前进
个单位长度,第三次再前进![]() 个单位长度,第四次又后退
个单位长度,第四次又后退![]() 个单位长度……按此规律行进,如果
个单位长度……按此规律行进,如果![]() 点在数轴上表示的数为
点在数轴上表示的数为![]() ,那么
,那么
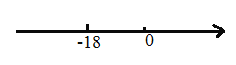
(1)求出![]() 点在数轴上表示的数.
点在数轴上表示的数.
(2)经过第七次行进后机器人到达点![]() ,第八次行进后到达点
,第八次行进后到达点![]() ,点
,点![]() 到
到![]() 点的距离相等吗?请说明理由.
点的距离相等吗?请说明理由.
(3)机器人在未到达![]() 点之前,经过
点之前,经过![]() 次(
次(![]() 为正整数)行进后,它在数轴上表示的数应如何用含
为正整数)行进后,它在数轴上表示的数应如何用含![]() 的代数式表示?
的代数式表示?
(4)如果![]() 点在原点的右侧,那么机器人经过
点在原点的右侧,那么机器人经过![]() 次行进后,它在
次行进后,它在![]() 点的什么位置?请通过计算说明.
点的什么位置?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB,AD为边分别向外侧作等边三角形ABF和等边三角形ADE,连接EB,FD,交点为G.
(1)当四边形ABCD为正方形时,如图①,EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时,如图②,EB和FD具有怎样的数量关系?请加以证明;
(3)如图③,四边形ABCD由正方形到矩形再到一般平行四边形的变化过程中,EB和FD具有怎样的数量关系?请直接写出结论,无需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明是个爱动脑筋的同学,在发现教材中的用方框在月历中移动的规律后,突发奇想,将连续的偶数2、4、6、8,…排成如下表,并用一个十字形框架住其中的五个数,请你仔细观察十字形框架中数字的规律,并回答下列问题:
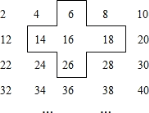
![]() 十字框中的五个数的和与中间的数16有什么关系?
十字框中的五个数的和与中间的数16有什么关系?
![]() 设中间的数为x,用代数式表示十字框中的五个数的和.
设中间的数为x,用代数式表示十字框中的五个数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=-2x与直线l2:y=kx+b在同一平面直角坐标系内交于点P .
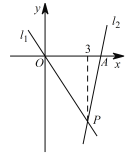
(1)直接写出不等式-2x>kx+b 的解集 ;
(2)设直线l2 与x 轴交于点A ,△OAP的面积为12 ,求l2的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com