
【题目】如图1,在△ABC中,按如下步骤作图:①以点A为圆心,AB长为半径画弧;②以点C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD.
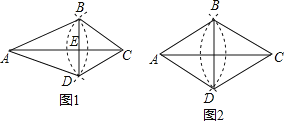
(1)填空:△ABC≌△ ;AC和BD的位置关系是
(2)如图2,当AB=BC时,猜想四边形ABCD是什么四边形,并证明你的结论.
(3)在(2)的条件下,若AC=8cm,BD=6cm,则点B到AD的距离是 cm,若将四边形ABCD通过割补,拼成一个正方形,那么这个正方形的边长为 cm.
【答案】(1)ADC(SSS),AC⊥BD;(2)四边形ABCD是菱形,见解析;(3)![]() ,2
,2![]() .
.
【解析】
(1)根据作法和三角形全等的判定方法解答,再根据到线段两端点距离相等的点在线段的垂直平分线上可得AC⊥BD;
(2)根据四条边都相等的四边形是菱形证明;
(3)设点B到AD的距离为h,然后根据菱形的面积等于底边×高和菱形的面积等于对角线乘积的一半列方程求解即可;再根据正方形的面积公式和菱形的面积求解.
(1)由图可知,AB=AD,CB=CD,
在△ABC和△ADC中,
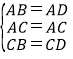 ,
,
∴△ABC≌△ADC(SSS),
∵AB=AD,
∴点A在BD的垂直平分线上,
∵CB=CD,
∴点C在BD的垂直平分线上,
∴AC垂直平分BD,
∴AC⊥BD;
(2)四边形ABCD是菱形.
理由如下:由(1)可得AB=AD,CB=CD,
∵AB=BC,
∴AB=BC=CD=DA,
∴四边形ABCD是菱形;
(3)设点B到AD的距离为h,
在菱形ABCD中,AC⊥BD,且AO=CO=4,BO=DO=3,
在Rt△ADO中,AD=![]() =5,
=5,
S菱形ABCD=![]() ACBD=ADh,
ACBD=ADh,
即![]() ×8×6=5h,
×8×6=5h,
解得h=![]() ,
,
设拼成的正方形的边长为a,则a2=![]() ×8×6,
×8×6,
解得a=2![]() cm.
cm.
所以,点B到AD的距离是![]() cm,拼成的正方形的边长为2
cm,拼成的正方形的边长为2![]() cm.
cm.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
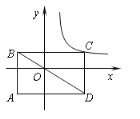
【题目】如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数![]() 的图象上.若点A的坐标为(-2,-2),则k的值为 。
的图象上.若点A的坐标为(-2,-2),则k的值为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教委为了让广大青少年学生走向操场、走进自然、走到阳光下,积极参加体育锻炼,启动了“学生阳光体育运动”,其中有一项是短跑运动,短跑运动可以锻炼人的灵活性,增强人的爆发力,因此张明和李亮在课外活动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
成绩统计分析表
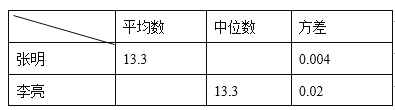
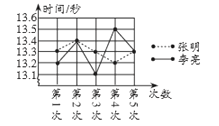
(1)张明第2次的成绩为__________秒;
(2)请补充完整上面的成绩统计分析表;
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁? 请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为20cm2,对角线交于点O,以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B2;…;依此类推,则平行四边形AO4C5B的面积为________,平行四边形AOnCn+1B的面积为________.
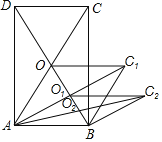
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=120°,△ABC是等边三角形,O点是边BC的中点,将△ABC绕点O逆时针旋转一定的角度,OM与边AB相交于点D,ON与边AC(或AC的延长线)相交于点E.
(1)如图1,若OD⊥AB,垂足为D,BC=4,求CE的长;
(2)如图2,当ON与AC边交于点E时,求证:BD+CE=![]() BC;
BC;
(3)如图3,当ON与AC边的延长线交于点E时,(2)中的结论还成立吗?如果成立,请证明;如果不成立,请直接写出线段BD、BC、CE之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c(b、c是常数)与x轴有两个交点,其中有一点的坐标为A(1,0),点P(m,t)(m≠0)为抛物线上的一个动点.
(1)设y′=m+t,写出y′关于m的函数解析式,并求出该函数图象的对称轴(用含c的代数式表示);
(2)在(1)的条件下,当m≤3时,与其对应的函数y′的最小值为﹣![]() ,求抛物线y=x2+bx+c的解析式;
,求抛物线y=x2+bx+c的解析式;
(3)在(2)的条件下,P点关于原点的对称点为P′,且P′落在第一象限内,当P′A2取得最小值时,求m与t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的道路AB上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,假设他们分别以不同的速度匀速行驶,甲先出发6分钟后,乙才出发,乙的速度为![]() 千米/分,在整个过程中,甲、乙两人之间的距离y(千米)与甲出发的时间x(分)之间的部分函数图象如图.
千米/分,在整个过程中,甲、乙两人之间的距离y(千米)与甲出发的时间x(分)之间的部分函数图象如图.
(1)A、B两地相距____千米,甲的速度为____千米/分;
(2)求线段EF所表示的y与x之间的函数表达式;
(3)当乙到达终点A时,甲还需多少分钟到达终点B?

查看答案和解析>>
科目:初中数学 来源: 题型:
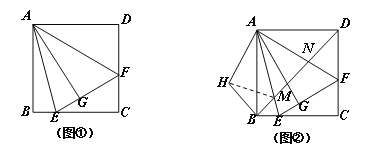
【题目】如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,
(1)求∠EAF的度数;
(2)在图①中,连结BD分别交AE、AF于点M、N,将△ADN绕点A顺时针旋转90°至△ABH位置,连结MH,得到图②.求证:MN2=MB2+ ND2 ;
(3)在图②中,若AG=12, BM=![]() ,直接写出MN的值.
,直接写出MN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
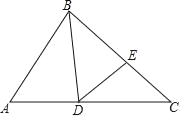
【题目】如图,BD是△ABC的角平分线,点E位于边BC上,已知BD是BA与BE的比例中项.
(1)求证:∠CDE=![]() ∠ABC;
∠ABC;
(2)求证:ADCD=ABCE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com