
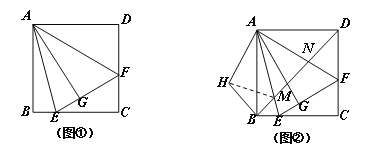
【题目】如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,
(1)求∠EAF的度数;
(2)在图①中,连结BD分别交AE、AF于点M、N,将△ADN绕点A顺时针旋转90°至△ABH位置,连结MH,得到图②.求证:MN2=MB2+ ND2 ;
(3)在图②中,若AG=12, BM=![]() ,直接写出MN的值.
,直接写出MN的值.
【答案】(1)45°;(2)证明见解析;(3)![]() .
.
【解析】(1)∵正方形ABCD,AG⊥EF,
∴AG=AB,∠ABE=∠AGE=∠BAD=90°,AE=AE,
∴Rt△ABE≌Rt△AGE,∴∠BAE=∠GAE,……………………………………2分
同理Rt△ADF≌Rt△AGF,∴∠GAF=∠DAF,…………………………………4分
∴∠EAF=![]() ∠BAD=45°;…………………………………………………………5分
∠BAD=45°;…………………………………………………………5分
(2)证明:由旋转知,∠BAH=∠DAN,AH=AN,……………………………………7分
∵∠BAD=90°,∠EAF=45°,∴∠BAM+∠DAN=45°,
∴∠HAM=∠BAM+∠BAH=∠BAM+∠DAN =45°,
∴∠HAM=∠NAM,AM=AM,
∴△AHM≌△ANM,…………………………………………………………………8分
∴MN=MH,∵四边形ABCD是正方形,∴∠ADB=∠ABD=45°
由旋转知,∠ABH=∠ADB=45°,HB=ND,
∴∠HBM=∠ABH+∠ABD=90°,……………………………………………………9分
∴![]() ,∴
,∴![]() ;…………………………………10分
;…………………………………10分
(3)![]() .…………………………………………………………………………………12分
.…………………………………………………………………………………12分
以下解法供参考∵![]() ,∴
,∴![]() ;
;
在(2)中, ![]()
设![]() ,则
,则![]() .
.
∴![]() .即
.即![]() .
.


科目:初中数学 来源: 题型:
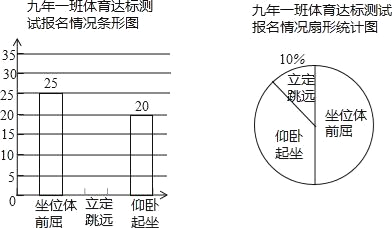
【题目】南岗区某中学的王老师统计了本校九年一班学生参加体育达标测试的报名情况,并把统计的数据绘制成了不完整的条形统计图和扇形统计图.根据图中提供的数据回答下列问题:
(1)该学校九年一班参加体育达标测试的学生有多少人?
(2)补全条形统计图的空缺部分;
(3)若该年级有1200名学生,估计该年级参加仰卧起坐达标测试的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,按如下步骤作图:①以点A为圆心,AB长为半径画弧;②以点C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD.
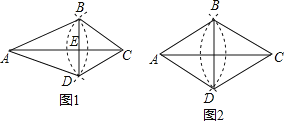
(1)填空:△ABC≌△ ;AC和BD的位置关系是
(2)如图2,当AB=BC时,猜想四边形ABCD是什么四边形,并证明你的结论.
(3)在(2)的条件下,若AC=8cm,BD=6cm,则点B到AD的距离是 cm,若将四边形ABCD通过割补,拼成一个正方形,那么这个正方形的边长为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】25 日某路段雷达测速区监测到一组汽车时速数据,经整理得到如下频数表和频数直方图(每组含后一边界值,不含前一边界值).
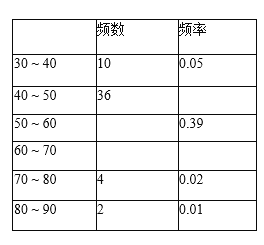
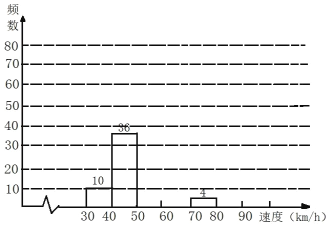
(1)请你把表中的数据填写完整.
(2)补全频数直方图.
(3)若该路段限速 70(汽车时速高于 70 千米/小时即为违章),抽测到违章车辆有多少辆?统计表明 25 日全天通过这个路段的汽车大约有 15000 辆,请估计这天超速违章的车辆有多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂计划每天生产零件![]() 个,但实际每天生产量与计划量相比有出入. 下表是某周的生产情况(超产数量记为正、减产数量记为负):
个,但实际每天生产量与计划量相比有出入. 下表是某周的生产情况(超产数量记为正、减产数量记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)由表可知该厂星期四生产零件 个,这周实际生产零件 个.(用含![]() 的代数式表示)
的代数式表示)
(2) 产量最高日比最低日多生产零件 个.
(3) 若该周厂计划每天生产零件数是![]() ,每个零件应支付工资
,每个零件应支付工资![]() 元,且每天超计划数的零件每个另奖
元,且每天超计划数的零件每个另奖![]() 元,那这周实际应支付工资多少元?
元,那这周实际应支付工资多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
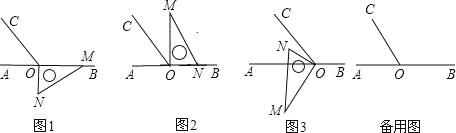
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为 度;
(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转到图3的位置的过程中,若三角板绕点O按15°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
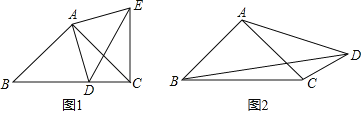
【题目】(1)如图1,在Rt△ABC和Rt△ADE中,AB=AC,AD=AE,且点D在BC边上滑动(点D不与点B,C重合),连接EC,
①则线段BC,DC,EC之间满足的等量关系式为 ;
②求证:BD2+CD2=2AD2;
(2)如图2,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=9,CD=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
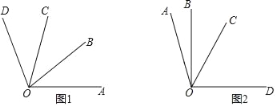
【题目】新定义:若∠α的度数是∠β的度数的n倍,则∠α叫做∠β的n倍角.
(1)若∠M=10°21′,请直接写出∠M的3倍角的度数;
(2)如图1,若∠AOB=∠BOC=∠COD,请直接写出图中∠AOB的所有2倍角;
(3)如图2,若∠AOC是∠AOB的3倍角,∠COD是∠AOB的4倍角,且∠BOD=90°,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
(1)求抛物线的解析式;
(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com