
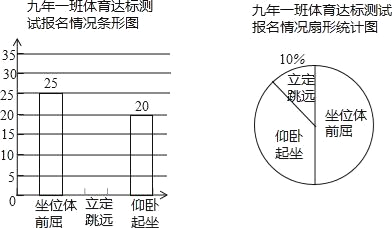
【题目】南岗区某中学的王老师统计了本校九年一班学生参加体育达标测试的报名情况,并把统计的数据绘制成了不完整的条形统计图和扇形统计图.根据图中提供的数据回答下列问题:
(1)该学校九年一班参加体育达标测试的学生有多少人?
(2)补全条形统计图的空缺部分;
(3)若该年级有1200名学生,估计该年级参加仰卧起坐达标测试的有多少人?
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】某乡A,B两村盛产香梨,A村有香梨200吨,B村有香梨300吨,现将这些香梨运到C,D两个冷藏仓库.已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C,D两处的费用分别为每吨40元和45元;从B村运往C,D两处的费用分别为每吨25元和32元.设从A村运往C仓库的香梨为x吨,A,B两村运香梨往两仓库的运输费用分别为yA元,yB元.
(1)请填写下表,并求出yA,yB与x之间的函数关系式;
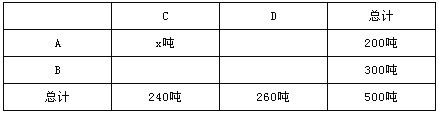
(2)当x为何值时,A村的运费较少?
(3)请问怎样调运,才能使两村的运费之和最小?求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
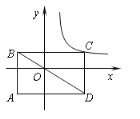
【题目】如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数![]() 的图象上.若点A的坐标为(-2,-2),则k的值为 。
的图象上.若点A的坐标为(-2,-2),则k的值为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
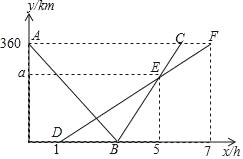
【题目】快、慢两车分别从相距360km的佳市、哈市两地出发,匀速行驶,先相向而行,慢车在快车出发1h后出发,到达佳市后停止行驶,快车到达哈市后,立即按原路原速返回佳市(快车调头的时间忽略不计),快、慢两车距哈市的路程y1(单位:km),y2(单位:km)与快车出发时间x(单位:h)之间的函数图象如图所示,请结合图象信息解答下列问题:
(1)直接写出慢车的行驶速度和a的值;
(2)快车与慢车第一次相遇时,距离佳市的路程是多少千米?
(3)快车出发多少小时后两车相距为100km?请直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点M在x轴上,以点M为圆心,2.5长为半径的圆交y轴于A、B两点,交x轴于C(x1,0)、D(x2,0)两点,(x1<x2),x1、x2是方程x(2x+1)=(x+2)2的两根.
(1)求点C、D及点M的坐标;
(2)若直线y=kx+b切⊙M于点A,交x轴于P,求PA的长;
(3)⊙M上是否存在这样的点Q,使点Q、A、C三点构成的三角形与△AOC相似?若存在,请求出点的坐标,并求出过A、C、Q三点的抛物线的解析式;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教委为了让广大青少年学生走向操场、走进自然、走到阳光下,积极参加体育锻炼,启动了“学生阳光体育运动”,其中有一项是短跑运动,短跑运动可以锻炼人的灵活性,增强人的爆发力,因此张明和李亮在课外活动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
成绩统计分析表
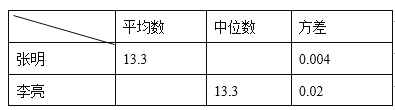
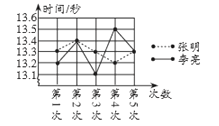
(1)张明第2次的成绩为__________秒;
(2)请补充完整上面的成绩统计分析表;
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁? 请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为20cm2,对角线交于点O,以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B2;…;依此类推,则平行四边形AO4C5B的面积为________,平行四边形AOnCn+1B的面积为________.
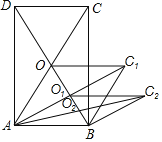
查看答案和解析>>
科目:初中数学 来源: 题型:
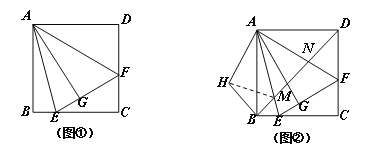
【题目】如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,
(1)求∠EAF的度数;
(2)在图①中,连结BD分别交AE、AF于点M、N,将△ADN绕点A顺时针旋转90°至△ABH位置,连结MH,得到图②.求证:MN2=MB2+ ND2 ;
(3)在图②中,若AG=12, BM=![]() ,直接写出MN的值.
,直接写出MN的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com