
����Ŀ����֪������y=x2+bx+c��b��c�dz�������x�����������㣬������һ�������ΪA��1��0������P��m��t����m��0��Ϊ�������ϵ�һ�����㣮
��1����y��=m+t��д��y������m�ĺ�������ʽ��������ú���ͼ��ĶԳ��ᣨ�ú�c�Ĵ���ʽ��ʾ����
��2���ڣ�1���������£���m��3ʱ�������Ӧ�ĺ���y������СֵΪ��![]() ����������y=x2+bx+c�Ľ���ʽ��
����������y=x2+bx+c�Ľ���ʽ��
��3���ڣ�2���������£�P�����ԭ��ĶԳƵ�ΪP������P�����ڵ�һ�����ڣ���P��A2ȡ����Сֵʱ����m��t��ֵ��
���𰸡���1��y��=m2��cm+c m=![]() c��2��y=x2+2x��3��3��t=��
c��2��y=x2+2x��3��3��t=��![]() m=
m=![]()
���������������������1�����ݵ�P��m��t����m��0��Ϊ�������ϵ�һ������ã�
t=m2+bm+c����y��=m+t=m+m2+bm+c=m2+��b+1��m+c��
��A��1��0������y=x2+bx+c����1+b+c=0��b+1=��c��
y��=m2��cm+c�����ݶ��κ����ĶԳ������ʽΪ���ú���ͼ��ĶԳ���Ϊm=![]() c��
c��
��2���ɣ�1��֪��y��=m2��cm+c���Գ���Ϊm=![]() c��
c��
��![]() c��3ʱ������c��6����ʱ��m=
c��3ʱ������c��6����ʱ��m=![]() cʱ��������y��=m2��cm+cȡ��Сֵ��
cʱ��������y��=m2��cm+cȡ��Сֵ��
����![]() c2��c��
c2��c��![]() c+c=��
c+c=��![]() ��
��
��ã�c=��3��c=7����ȥ����
��c=��3ʱ��b=��c��1=2��
��y=x2+2x��3��
��3����y=x2+2x��3ʱ��
��P����ԭ��ĶԳƵ�ΪP'����P'����m����t����
��P'����m����t���ڵ�һ���ޣ�
����m��0����t��0����m��0��t��0��
��������y=x2+2x��3�Ķ���Ϊ����1����4��
����4��t��0��
��A��������1��0����
���������ľ��빫ʽ�ã�P'A2=����m��1��2+t2=��m+1��2+t2��
��t=m2+2m��3=��m+1��2��4��
������m+1��2=t+4��
��P'A2=t2+t+4=��t+![]() ��2+
��2+![]()
�൱t=��![]() ʱ��P'A2ȡ����Сֵ��
ʱ��P'A2ȡ����Сֵ��
��t=��![]() ����t=m2+2m��3���é�
����t=m2+2m��3���é�![]() =m2+2m��3
=m2+2m��3
���m=![]() ��m=
��m=![]() ���ᣩ
���ᣩ
�ʣ���t=��![]() ʱ��m=
ʱ��m=![]() .
.
�����������
��1����t=m2+bm+c��
��y��=m+t=m+m2+bm+c=m2+��b+1��m+c��
��A��1��0������y=x2+bx+c����1+b+c=0��b+1=��c��
��y��=m2��cm+c��
��ú���ͼ��ĶԳ���Ϊm=![]() c��
c��
��2���ɣ�1��֪��y��=m2��cm+c���Գ���Ϊm=![]() c��
c��
��![]() c��3ʱ������c��6����ʱ��m=3ʱ��������y��=m2��cm+cȡ��Сֵ��
c��3ʱ������c��6����ʱ��m=3ʱ��������y��=m2��cm+cȡ��Сֵ��
�ߵ�P��m��t����
���P�������3��
������P�Ƕ��㣬���Ƕ��㣬���������⣬
��![]() c��3ʱ������c��6����ʱ��m=
c��3ʱ������c��6����ʱ��m=![]() cʱ��������y��=m2��cm+cȡ��Сֵ��
cʱ��������y��=m2��cm+cȡ��Сֵ��
����![]() c2��c��
c2��c��![]() c+c=��
c+c=��![]() ��
��
��c=��3��c=7����ȥ����
��c=��3ʱ��b=��c��1=2��
��y=x2+2x��3��
��3����y=x2+2x��3ʱ��
��P����ԭ��ĶԳƵ�ΪP'����P'����m����t����
��P'����m����t���ڵ�һ���ޣ�
����m��0����t��0����m��0��t��0��
��������y=x2+2x��3�Ķ���Ϊ����1����4��
����4��t��0��
��A��������1��0����
��P'A2=����m��1��2+t2=��m+1��2+t2��
��t=m2+2m��3=��m+1��2��4��
����m+1��2=t+4��
��P'A2=t2+t+4=��t+![]() ��2+
��2+![]()
�൱t=��![]() ʱ��P'A2ȡ����Сֵ��
ʱ��P'A2ȡ����Сֵ��
��t=��![]() ����t=m2+2m��3���é�
����t=m2+2m��3���é�![]() =m2+2m��3
=m2+2m��3
���m=![]() ��m=
��m=![]() ���ᣩ
���ᣩ
�൱t=��![]() ʱ��m=
ʱ��m=![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��㳧�����ǰҪ����һ����װ�±���ÿ����װ2����±���4��С�±�������1����±�Ҫ��0.05kg��ۣ�1��С�±�Ҫ��0.02kg��ۣ��ֹ������4500kg�������������±�Ӧ���ö�����ۣ������������ĺ�װ�±�������һԪһ�η��̽��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a�����ĸ�������b��-5���෴����c=-|-2|����a��b��c�ֱ��ǵ�A��B��C�������϶�Ӧ������
![]()
��1����a��b��c��ֵ�����������ϱ����A��B��C��
��2��������P�ӵ�A�����������������˶�������Qͬʱ�ӵ�B����Ҳ�������������˶�����P���ٶ���ÿ��3����λ���ȣ���Q���ٶ���ÿ��1����λ���ȣ����˶������P�����ϵ�Q��
��3������������һ��M��ʹ��M��A��B��C����ľ���֮�͵���12����������е�M��Ӧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ĩ��С���ӼҲ���ȥ��꿴��.����![]() Сʱ����1.8ǧ��ʱ���ְּݳ��Ӽ�����ͬ·����С������
Сʱ����1.8ǧ��ʱ���ְּݳ��Ӽ�����ͬ·����С������![]() ����С�����˼ݳ�����ǰ�е������.С�������
����С�����˼ݳ�����ǰ�е������.С�������![]() ���飬�ְ�ȥ��λ
���飬�ְ�ȥ��λ![]() �ذ���.��ͼ��С����ְ�����֮�����
�ذ���.��ͼ��С����ְ�����֮�����![]() ��ǧ�ף���С��������ʱ��
��ǧ�ף���С��������ʱ��![]() ��Сʱ��֮��ĺ���ͼ��С�������ٶ���ְּݳ��ٶ�ʼ�ձ��ֲ��䣬�˴˽���ʱ����Բ��ƣ��������ͼ��ش��������⣺
��Сʱ��֮��ĺ���ͼ��С�������ٶ���ְּݳ��ٶ�ʼ�ձ��ֲ��䣬�˴˽���ʱ����Բ��ƣ��������ͼ��ش��������⣺
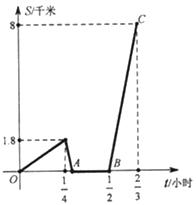
��1��С�������ٶ���_____ǧ��/Сʱ���ְּݳ��ٶ���______ǧ��/Сʱ��
��2��ͼ�е�![]() ��������______��
��������______��
��3���������ҵ�·�̣�
��4����ְֳ����ʱ�䣬�������3ǧ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڡ�ABC�У������²�����ͼ�����Ե�AΪԲ�ģ�AB��Ϊ�뾶���������Ե�CΪԲ�ģ�CB��Ϊ�뾶�����������ཻ�ڵ�D��������BD����AC���ڵ�E������AD��CD��
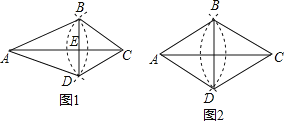
��1����գ���ABC�ա� ��AC��BD��λ�ù�ϵ��
��2����ͼ2����AB=BCʱ�������ı���ABCD��ʲô�ı��Σ���֤����Ľ��ۣ�
��3���ڣ�2���������£���AC=8cm��BD=6cm�����B��AD�ľ����� cm�������ı���ABCDͨ�����ƴ��һ�������Σ���ô��������εı߳�Ϊ cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��ѧ����ͣ��� 400g��Ӫ���ɷ�����ͳ��ͼ����֪���б�ʾ֬�������ε�Բ�Ľ�Ϊ 36����ά���غͿ����ʺ���ռ֬����һ �룬�����ʺ�����̼ˮ������� 40g.�й���ݿ�ͣ�����˵���� ȷ���ǣ� ��

A.��ʾά���غͿ����ʵ����ε�Բ�Ľ�Ϊ 20��.B.֬���� 44g���������� 10%.
C.��ʾ̼ˮ����������ε�Բ�Ľ�Ϊ 135��.D.�����ʵĺ���Ϊά���غͿ����ʵ� 9 ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��25 ��ij·���״��������һ������ʱ�����ݣ��������õ�����Ƶ������Ƶ��ֱ��ͼ��ÿ�麬��һ�߽�ֵ������ǰһ�߽�ֵ��.
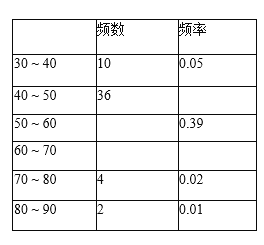
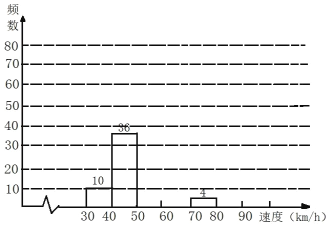
��1������ѱ��е�������д����.
��2����ȫƵ��ֱ��ͼ.
��3������·������ 70������ʱ�ٸ��� 70 ǧ��/Сʱ��ΪΥ�£�����Υ�³����ж�������ͳ�Ʊ��� 25 ��ȫ��ͨ�����·�ε�������Լ�� 15000 ������������쳬��Υ�µij����ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����OΪֱ��AB��һ�㣬��O��������OC��ʹ��AOC����BOC��1��2����һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����һ��OM������OB�ϣ���һ��ON��ֱ��AB���·���
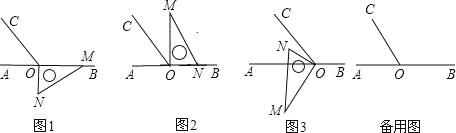
��1����ͼ1�е����ǰ��Ƶ�O����ʱ�뷽����ת��ͼ2��λ�ã�ʹ��ON��������OB�ϣ���ʱ���ǰ���ת�ĽǶ�Ϊ�� ���ȣ�
��2��������ͼ2�е����ǰ��Ƶ�O����ʱ�뷽����ת��ͼ3��λ�ã�ʹ��ON�ڡ�AOC���ڲ�����̽����AOM���NOC֮������ʲô������ϵ����˵�����ɣ�
��3��������ֱ�����ǰ��ͼ1��ʱ����ת��ͼ3��λ�õĹ����У������ǰ��Ƶ�O��15��ÿ����ٶ���ת����ֱ�����ǰ��ֱ�DZ�ON����ֱ��ǡ��ƽ�֡�AOCʱ�����ʱ���ǰ��Ƶ�O���˶�ʱ��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬABCD����E�ڱ�AB�ϣ�M��N�ֱ�������BC������AD�ϣ�����EM��EN����������MBE��EM�۵����������һ���ַ�ת����һ������£������B���ڵ�B��������������NAE��EN�۵�����A���ڵ�A����.
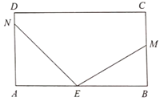
��1����![]() ��
��![]() ����ֱ�ߡ���������������EB����EA����
����ֱ�ߡ���������������EB����EA����
��2����![]() ��
��![]() ����
����![]() �Ķ�����
�Ķ�����
��3����![]() ��
��![]() ���ú�
���ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() �Ķ���.
�Ķ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com