
����Ŀ����֪a�����ĸ�������b��-5���෴����c=-|-2|����a��b��c�ֱ��ǵ�A��B��C�������϶�Ӧ������
![]()
��1����a��b��c��ֵ�����������ϱ����A��B��C��
��2��������P�ӵ�A�����������������˶�������Qͬʱ�ӵ�B����Ҳ�������������˶�����P���ٶ���ÿ��3����λ���ȣ���Q���ٶ���ÿ��1����λ���ȣ����˶������P�����ϵ�Q��
��3������������һ��M��ʹ��M��A��B��C����ľ���֮�͵���12����������е�M��Ӧ������
���𰸡���1��a=-1��b=5��c=-2���������������2���˶�3���P�����ϵ�Q����3����M��Ӧ������-3![]() ��4��
��4��
��������
��1���������������෴��������ֵ�йظ���ܹ���ȷ�������ᣬ��ȷ���������ҵ�����Ӧ�ĵ㣻
��2�����������������ľ����������⣻
��3��ע�������������ľ��빫ʽ����������Ӧ�����IJ�ľ���ֵ��
��1��a�����ĸ���������a=-1��
b��-5���෴������b=5��
c=-|-2|=-2��
���Ե�A��B��C��������λ����ͼ��ʾ��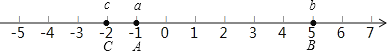
��2�����˶�t���P�����ϵ�Q��
���P��ʾ��-1+3t����Q��ʾ5+t��
������ã�-1+3t=5+t��
��ã�t=3��
���˶�3���P�����ϵ�Q��
��3�����ڵ�M��ʹM��A��B��C����ľ���֮�͵���12��a=-1��b=5��c=-2��
��M��C����࣬��M��Ӧ�����ǣ�-1-m+5-m-2-m=12,m=-3![]() ��
��
��M��AB֮�䣬��M��Ӧ������:m+2+m+1+5-m=12,m=4��
��ʹ��M��A��B��C����ľ���֮�͵���12����M��Ӧ������-3![]() ��4��
��4��


 �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д� С����ȫ�ܼ��ϵ�д�
С����ȫ�ܼ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������A��B��Ӧ�����ֱ�Ϊ��2��7����MΪ������һ���㣮
��1���뻭�����ᣬ���������ϱ����A����B��
��2������M��A�ľ����ǵ�M��B�ľ�������������ǾͳƵ�M�ǣ�A��B���ĺõ㣮
������M�˶���ԭ��Oʱ����ʱ��M�� ����A��B���ĺõ㣨���ǻ��߲��ǣ�
������M��ÿ��1����λ���ٶȴ�ԭ��O��ʼ�˶�����M�ǣ�B��A���ĺõ�ʱ�����M���˶�������˶�ʱ��
��3����̽���߶�BM��AM�IJBM��AM��ֵ�Ƿ�һ�������仯�����仯����˵�����ɣ������䣬������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ڱ�ֱ�ĺ��߹�·��ͬ��㡢ͬ�յ㡢ͬ�������ٲ���2400�ף��ȵ��յ����ԭ����Ϣ����֪���ȳ���4���ӣ����������й����У��ס������˵ľ���y���ף���׳�����ʱ��t���֣�֮��Ĺ�ϵ��ͼ��ʾ�����н��ۣ�
���ײ��е��ٶ�Ϊ60��/�֣�
��������ȫ������32���ӣ�
������16�����ϼף�
���ҵ����յ�ʱ�������յ㻹��300��
������ȷ�Ľ����У�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����M��x���ϣ��Ե�MΪԲ�ģ�2.5��Ϊ�뾶��Բ��y����A��B���㣬��x����C��x1��0����D��x2��0�����㣬��x1��x2����x1��x2�Ƿ���x��2x+1��=��x+2��2��������
��1�����C��D����M�����ꣻ
��2����ֱ��y=kx+b�С�M�ڵ�A����x����P����PA�ij���
��3����M���Ƿ���������ĵ�Q��ʹ��Q��A��C���㹹�ɵ�����������AOC���ƣ������ڣ������������꣬�������A��C��Q����������ߵĽ���ʽ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н�ίΪ���ù��������ѧ������ٳ����߽���Ȼ���ߵ������£������μ�������������������ѧ�����������˶�����������һ���Ƕ����˶��������˶����Զ����˵�����ԣ���ǿ�˵ı���������������������ڿ����б����μ��˰���ѵ��С��.�ڽ����ΰ���ѵ���У��������������˵IJ��Գɼ�������ͳ�ƺͷ����������ͼ���е���Ϣ����������⣺
�ɼ�ͳ�Ʒ�����
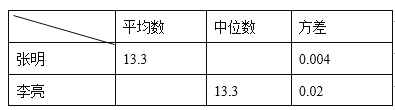
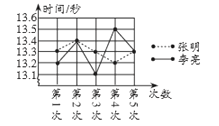
��1��������2�εijɼ�Ϊ__________�룻
��2���벹����������ijɼ�ͳ�Ʒ�������
��3�����ڴ�������������ѡ��һ���ɼ������ȥ�μӱ��������������ǵĽ�����Ӧ��ѡ��˭�� ��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ������C�ڰ�Բ�⣬AC��BC���Բ����D���E�㣮
��1����ֻ���̶ȵ�ֱ��������ABC���������ߣ���д��������
��2����AC=AB������DE��BE����֤��DE=BE��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�����Ϊ20cm2���Խ��߽��ڵ�O����AB��AOΪ�ڱ���ƽ���ı���AOC1B���Խ��߽��ڵ�O1����AB��AO1Ϊ�ڱ���ƽ���ı���AO1C2B2�������������ƣ���ƽ���ı���AO4C5B�����Ϊ________��ƽ���ı���AOnCn+1B�����Ϊ________��
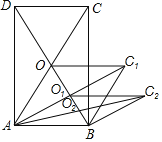
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=x2+bx+c��b��c�dz�������x�����������㣬������һ�������ΪA��1��0������P��m��t����m��0��Ϊ�������ϵ�һ�����㣮
��1����y��=m+t��д��y������m�ĺ�������ʽ��������ú���ͼ��ĶԳ��ᣨ�ú�c�Ĵ���ʽ��ʾ����
��2���ڣ�1���������£���m��3ʱ�������Ӧ�ĺ���y������СֵΪ��![]() ����������y=x2+bx+c�Ľ���ʽ��
����������y=x2+bx+c�Ľ���ʽ��
��3���ڣ�2���������£�P�����ԭ��ĶԳƵ�ΪP������P�����ڵ�һ�����ڣ���P��A2ȡ����Сֵʱ����m��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��������ı���չ��ͼ,ÿ������涼��ע����ĸ,�����Ҫ��ش�����:
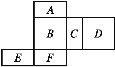
(1)�����A�ڶ�����ĵײ�,��ô��һ�����������?
(2)�����F��ǰ��,�����濴����B,��ô��һ�����������?
(3)��������濴����C,��D�ں���,��ô��һ�����������?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com