
【题目】如图,二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.
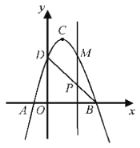
(1)求二次函数的解析式和直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴垂线,交抛物线于点
轴垂线,交抛物线于点![]() ,当点
,当点![]() 在第一象限时,求线段
在第一象限时,求线段![]() 长度的最大值;
长度的最大值;
(3)在抛物线上是否存在异于![]() 、
、![]() 的点
的点![]() ,使
,使![]() 中
中![]() 边上的高
边上的高![]() ?若存在求出点
?若存在求出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
【答案】(1)抛物线![]() ,直线AD
,直线AD![]()
(2)PM的最大值是![]() ,(3)存在,
,(3)存在,![]()
【解析】
(1)可设抛物线解析式为顶点式,由B点坐标可求得抛物线的解析式,则可求得A,D点坐标,利用待定系数法可求得直线AD解析式; (2)设出P点坐标,从而可表示出PM的长度,利用二次函数的性质可求得其最大值; (3)过Q作QG∥y轴,交BD于点G,过Q和QH⊥BD于H,可设出Q点坐标,表示出QG的长度,由条件可证得△DHG为等腰直角三角形,则可得到关于Q点坐标的方程,可求得Q点坐标.
解: (1)∵抛物线的顶点C的坐标为(1,4),
∴可设抛物线解析式为![]() ,
,
∵点B(3,0)在该抛物线的图象上,
∴![]() ,解得a=-1,
,解得a=-1,
∴抛物线解析式为![]() ,即
,即![]() ,
,
∵点D在y轴上,令x=0可得y=3, ∴D点坐标为(0,3),
令![]() ,得
,得![]() ,所以
,所以![]()
![]()
∴可设直线AD解析式为y=kx+3,
把A点坐标代入可得-k+3=0,解得k=3,
∴直线AD解析式为![]() ;
;
(2)因为B(3,0),D(0,3),所以直线BD为![]() ,
,
设P点横坐标为m(m>0),则P(m,-m+3),![]() ,
,
∴PM=![]() ,
,
∴当m=![]() 时,PM有最大值
时,PM有最大值![]() ;
;
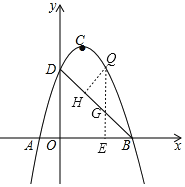
设Q![]() ,则G
,则G![]() ,
,
∴QG=![]() ,
,
∵△BOD是等腰直角三角形, ∴∠DBO=45°, ∴∠HGQ=∠BGE=45°,
当△BDQ中BD边上的高为![]() 时,即QH=HG=
时,即QH=HG=![]() ,
,
∴QG=![]() , ∴
, ∴![]() ,
,
当![]() 时,△=9-16<0,方程无实数根,
时,△=9-16<0,方程无实数根,
当![]() 时,解得x=-1或x=4,
时,解得x=-1或x=4,
∴Q(-1,0)或(4,-5),
综上可知存在满足条件的点Q,其坐标为(-1,0)或(4,-5).


科目:初中数学 来源: 题型:
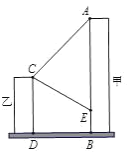
【题目】我市在创建全国文明城市的过程中,某社区在甲楼的![]() 处与
处与![]() 处之间悬挂了一幅宣传条幅,在乙楼顶部点测得条幅顶端
处之间悬挂了一幅宣传条幅,在乙楼顶部点测得条幅顶端![]() 点的仰角为45°,测得条幅底端
点的仰角为45°,测得条幅底端![]() 点的俯角为30°,若甲、乙两楼之间的水平距离
点的俯角为30°,若甲、乙两楼之间的水平距离![]() 为12米.
为12米.
(1)甲楼比乙楼高多少米?
(2)求条幅AE的长度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
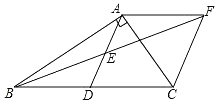
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:四边形ADCF是菱形;
(2)若AC=12,AB=16,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
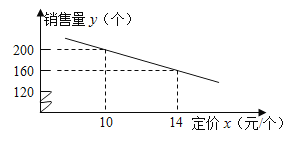
【题目】丹尼斯超市进了一批成本为 8 元/个的文具盒. 调查发现:这种文具盒每个星期的销售量y(个)与它的定价 x(元/个)的关系如图所示:
(1)求这种文具盒每个星期的销售量 y(个)与它的定价 x(元/个)之间的函数关系式(不必写出自变量 x的取值范围);
(2)每个文具盒的定价是多少元,超市每星期销售这种文具盒 (不考虑其他因素)可或得的利润为 1200 元?
(3)若该超市每星期销售这种文具盒的销售量小于 115 个, 且单件利润不低于 4 元(x 为整数),当每个文具盒定价多少 元时,超市每星期利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:![]() 与x轴交于点
与x轴交于点![]() ,与y轴交于点B,点C是线段OA上一动点
,与y轴交于点B,点C是线段OA上一动点![]() 以点A为圆心,AC长为半径作
以点A为圆心,AC长为半径作![]() 交x轴于另一点D,交线段AB于点E,连结OE并延长交
交x轴于另一点D,交线段AB于点E,连结OE并延长交![]() 于点F.
于点F.
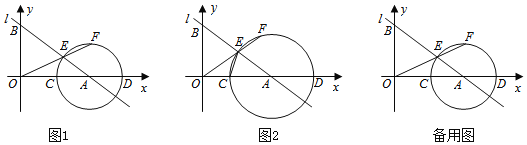
![]() 求直线l的函数表达式和
求直线l的函数表达式和![]() 的值;
的值;
![]() 如图2,连结CE,当
如图2,连结CE,当![]() 时,
时,
![]() 求证:
求证:![]() ∽
∽![]() ;
;
![]() 求点E的坐标;
求点E的坐标;
![]() 当点C在线段OA上运动时,求
当点C在线段OA上运动时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
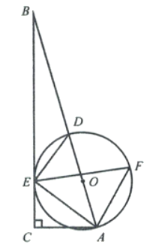
【题目】如图,在△ABC中,∠C=90°,O是AB上一点,以O为圆心,OA为半径作圆与BC相切于点E,交AB于点D,连接DE,作∠DEA的平分线EF交⊙O于点F,连接AF.
(1)求证:AE平分∠BAC
(2)若sin∠EFA=![]() ,AF=
,AF=![]() ,求线段AC的长
,求线段AC的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为![]() 小时,两车之间的距离为
小时,两车之间的距离为![]() 千米,图中折线表示
千米,图中折线表示![]() 与
与![]() 之间的函数图象.当快车到达甲地时,慢车离甲地的距离为__________千米.
之间的函数图象.当快车到达甲地时,慢车离甲地的距离为__________千米.
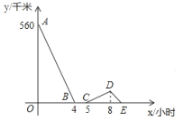
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公历3月12日是植树节,为宣传保护数目,激发人们爱林造林的热情,政府投资13万元给某村民小组用于购买与种植![]() 两种树苗共3000棵,完成这项种植后,剩余的款项作为村民小组的纯收入,已知用160元购买
两种树苗共3000棵,完成这项种植后,剩余的款项作为村民小组的纯收入,已知用160元购买![]() 树苗比购买
树苗比购买![]() 树苗多3棵,这两种树苗的单价、成活率及移栽费用见下表:
树苗多3棵,这两种树苗的单价、成活率及移栽费用见下表:
(1)求表中![]() 的值;
的值;
(2)设购买![]() 树苗
树苗![]() 棵,其它购买的是
棵,其它购买的是![]() 树苗,把这些树苗种植完成后,村民小组获得的纯收入为
树苗,把这些树苗种植完成后,村民小组获得的纯收入为![]() 元,请你写出
元,请你写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若要求这批树苗种植后,成活率达到93%以上(包含93%),则最多种植![]() 树苗多少棵?此时,村民小组在这项工作中,所得的纯收入最大值可以是多少元?
树苗多少棵?此时,村民小组在这项工作中,所得的纯收入最大值可以是多少元?
树苗品种 |
|
|
购买价格(元/棵) |
|
|
树苗成活率 | 90% | 95% |
移栽费用(元/棵) | 3 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com