
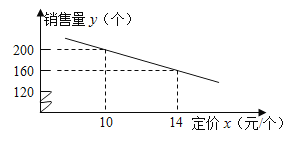
【题目】丹尼斯超市进了一批成本为 8 元/个的文具盒. 调查发现:这种文具盒每个星期的销售量y(个)与它的定价 x(元/个)的关系如图所示:
(1)求这种文具盒每个星期的销售量 y(个)与它的定价 x(元/个)之间的函数关系式(不必写出自变量 x的取值范围);
(2)每个文具盒的定价是多少元,超市每星期销售这种文具盒 (不考虑其他因素)可或得的利润为 1200 元?
(3)若该超市每星期销售这种文具盒的销售量小于 115 个, 且单件利润不低于 4 元(x 为整数),当每个文具盒定价多少 元时,超市每星期利润最高?最高利润是多少?
【答案】解:(1)![]() ;(2)当定价为18元或20元时,利润为1200元;(3)每个文具盒的定价是18元时,可获得每星期最高销售利润1200元.
;(2)当定价为18元或20元时,利润为1200元;(3)每个文具盒的定价是18元时,可获得每星期最高销售利润1200元.
【解析】
试题(1)由图可设函数关系式为![]() ,由图象过点(10,200)(14,160)即可根据待定系数法求解;
,由图象过点(10,200)(14,160)即可根据待定系数法求解;
(2)根据等量关系:总利润=单利润×总数量,即可列方程求解;
(3)先根据“每星期销售这种文具盒的销售量不少于115个,且单件利润不低于4元”求得x的取值范围,再根据等量关系:总利润=单利润×总数量,得到超市每星期的利润W与x的函数关系式,最后根据二次函数的性质求解即可.
(1)y=-10x+300;
(2)(x-8)·y=(x-8)(-10x+300)="1200"
解之得![]()
答:当定价为18元或20元时,利润为1200元;
(3)根据题意得:![]() ,
,![]()
得![]() ,且
,且![]() 为整数
为整数
设每星期所获利润为W元
则W=(x-8)·y=(x-8)(-10x+300)=-10(x2-38x+240)=-10(x-19) 2+1210
当x=18时,W有最大值, W最大=1200
每个文具盒的定价是18元时,可获得每星期最高销售利润1200元.


科目:初中数学 来源: 题型:
【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )

A. ![]() B. 2
B. 2![]() -
-![]() C. 2
C. 2![]() -
-![]() D. 4
D. 4![]() -
-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数![]() 的图象的一支在第一象限,A(﹣1,a)、B(﹣3,b)均在这个函数的图象上.
的图象的一支在第一象限,A(﹣1,a)、B(﹣3,b)均在这个函数的图象上.
(1)图象的另一支位于什么象限?常数n的取值范围是什么?
(2)试比较a、b的大小;
(3)作AC⊥x轴于点C,若△AOC的面积为5,求这个反比例函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
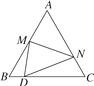
【题目】如图,等边△ABC的边长为30,点M为线段AB上一动点,将等边△ABC沿过点M的直线折叠,使点A落在直线BC上的点D处,且BD∶DC=1∶4,折痕与直线AC交于点N,则AN的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
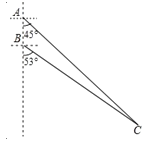
【题目】如图所示,我国两艘海监船 A,B 在南海海域巡逻,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船 C,此时,B 船在A 船的正南方向 15 海里处,A 船测得渔船 C 在其南偏东 45°方向,B 船测得渔船 C 在其南偏东 53°方向,已知 A 船的航速为 30 海里/小时,B 船的航速为 25 海里/小时,问 C 船至少要等待多长时间才能得到救援?(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈ 4 ,
,tan53°≈ 4 ,![]() 1.41 )
1.41 )
查看答案和解析>>
科目:初中数学 来源: 题型:
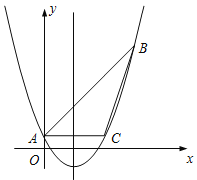
【题目】如图,已知抛物线 y![]() x2 bxc经过△ ABC 的三个顶点,其中点 A(0,1),点 B(9,10),AC∥x 轴,点 P 是直线 AC 下方抛物线上的动点,过点 P 且与 y 轴平行的直线 l 与直线 AB、AC 分别交于点 E、F.
x2 bxc经过△ ABC 的三个顶点,其中点 A(0,1),点 B(9,10),AC∥x 轴,点 P 是直线 AC 下方抛物线上的动点,过点 P 且与 y 轴平行的直线 l 与直线 AB、AC 分别交于点 E、F.
(1)求抛物线的函数表达式;
(2)如图 1,当四边形 AECP 的面积最大时,求点 P 的坐标和四边形 AECP 的最大面积;
(3)如图 2,当点 P 为抛物线的顶点时,在直线 AC 上是否存在点 Q,使得以 C,P,Q 为顶点的三角形与△ ABC 相似?若存在,请直接写出点 Q 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个工人拿一个![]() 米长的梯子,底端
米长的梯子,底端![]() 放在距离墙根
放在距离墙根![]() 点
点![]() 米处,另一端点
米处,另一端点![]() 点靠墙.
点靠墙.
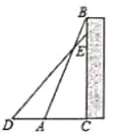
(1)求这个梯子的顶端距离地面的高度![]() ;
;
(2)如图,如果梯子的顶部下滑![]() 米,那么梯子的底部向外滑多少米.
米,那么梯子的底部向外滑多少米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的三张形状相同、大小完全相同的方格纸,方格纸中每个小正方形的边长为1,请依次在3个图中画出满足要求的三角形,要求所画的三角形的各顶点必须与方格纸中小正方形的顶点重合.
(1)画一个底边长为4,面积为10的等腰三角形;
(2)画一个面积为10的等腰直角三角形;
(3)画一个一边长为2![]() 且面积为10的等腰三角形.
且面积为10的等腰三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com