练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，一个工人拿一个米长的梯子，底端放在距离墙根点米处，另一端点点靠墙．

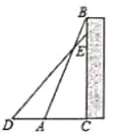
    （1）求这个梯子的顶端距离地面的高度；

    （2）如图，如果梯子的顶部下滑米，那么梯子的底部向外滑多少米．

    【答案】（1）2.4米；（2）0.8米．

    【解析】

    （1）首先在直角三角形ABC中计算出CB长；
    （2）由题意可得EC长，再次在直角三角形EDC中计算出DC长，从而可得AD的长度．

    （1）∵AB=2.5米，AC=0.7米，
    ∴BC==2.4（米），
    答：这个梯子的顶端距离地面的高度BC为2.4米；
    （2）∵梯子的顶部下滑0.4米，
    ∴BE=0.4米，
    ∴EC=BC-0.4=2米，
    ∴DC= =1.5米．
    ∴梯子的底部向外滑出AD=1.5-0.7=0.8（米）．
    答：梯子的底部向外滑0.8米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】有一类随机事件概率的计算方法：设试验结果落在某个区域S中的每一点的机会均等，用A表示事件“试验结果落在S中的一个小区域M中”，那么事件A发生的概率P（A）=． 有一块边长为30cm的正方形ABCD飞镖游戏板，假设飞镖投在游戏板上的每一点的机会均等．求下列事件发生的概率：

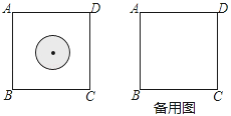
    (1)在飞镖游戏板上画有半径为5cm的一个圆（如图1），求飞镖落在圆内的概率；

    (2)飞镖在游戏板上的落点记为点O，求△OAB为钝角三角形的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

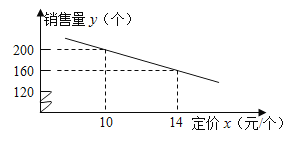
    【题目】丹尼斯超市进了一批成本为 8 元/个的文具盒. 调查发现：这种文具盒每个星期的销售量y(个)与它的定价 x(元/个)的关系如图所示：

    (1)求这种文具盒每个星期的销售量 y(个)与它的定价 x(元/个)之间的函数关系式(不必写出自变量 x的取值范围)；

    (2)每个文具盒的定价是多少元，超市每星期销售这种文具盒 (不考虑其他因素)可或得的利润为 1200 元?

    (3)若该超市每星期销售这种文具盒的销售量小于 115 个， 且单件利润不低于 4 元(x 为整数)，当每个文具盒定价多少 元时，超市每星期利润最高?最高利润是多少?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学为了解学生对新闻、体育、娱乐、动画四类电视节目的喜爱情况，进行了统计调查随机调查了某班所有同学最喜欢的节目每名学生必选且只能选择四类节目中的一类并将调查结果绘成如下不完整的统计图根据两图提供的信息，回答下列问题：

    最喜欢娱乐类节目的有______人，图中______；

    请补全条形统计图；

    根据抽样调查结果，若该校有1800名学生，请你估计该校有多少名学生最喜欢娱乐类节目；

    在全班同学中，有甲、乙、丙、丁等同学最喜欢体育类节目，班主任打算从甲、乙、丙、丁4名同学中选取2人参加学校组织的体育知识竞赛，请用列表法或树状图求同时选中甲、乙两同学的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

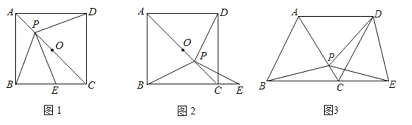
    【题目】如图，点P是正方形ABCD对角线AC上一动点，点E在射线BC上，且PE＝PB，连接PD，O为AC中点．

    （1）如图1，当点P在线段AO上时，试猜想PE与PD的数量关系和位置关系，请说明理由；

    （2）①如图2，当点P在线段OC上时，（1）中的猜想还成立吗？请说明理由；

    ②如图2，试用等式来表示PB,BC,CE之间的数量关系，并证明．

    （3）如图3，把正方形ABCD改为菱形ABCD，其他条件不变，当时，连接DE，试探究线段PB与线段DE的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在直角坐标系中（，，三点在正方形网格的交点上）按如图所示的方式放置，请解答下列问题：

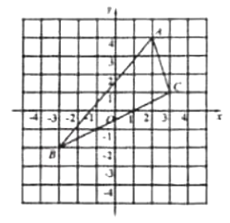
    （1），，三点的坐标分别为：____________，_____________，____________；

    （2）点关于轴对称的点为点，则点的坐标为______________；

    点关于轴对称的点为点，则点的坐标为____________；

    将点向下移动得到点，若直线轴，则点的坐标为______________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D．

    （1）求证：AC2＝ADAB；

    （2）求证：AC2+BC2＝AB2（即证明勾股定理）；

    （3）如果AC＝4，BC＝9，求AD：DB的值；

    （4）如果AD＝4，DB＝9，求AC：BC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形纸片ABCD中，AB=8，AD=6，折叠纸片使AD边与对角线BD重合，折痕为DG，则线段A'B的长度为____，折痕DG的长度为____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线的对称轴为直线，且抛物线与轴交于、两点，与轴交于点，其中，.

    （1）若直线经过、两点，求直线和抛物线的解析式；

    （2）在抛物线的对称轴上找一点，使点到点的距离与到点的距离之和最小，求出点的坐标；

    （3）设点为抛物线的对称轴上的一个动点，求使为直角三角形的点的坐标.

    查看答案和解析>>

    同步练习册答案