
【题目】如图的三张形状相同、大小完全相同的方格纸,方格纸中每个小正方形的边长为1,请依次在3个图中画出满足要求的三角形,要求所画的三角形的各顶点必须与方格纸中小正方形的顶点重合.
(1)画一个底边长为4,面积为10的等腰三角形;
(2)画一个面积为10的等腰直角三角形;
(3)画一个一边长为2![]() 且面积为10的等腰三角形.
且面积为10的等腰三角形.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
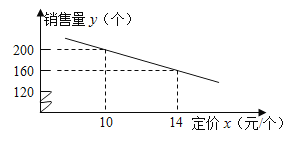
【题目】丹尼斯超市进了一批成本为 8 元/个的文具盒. 调查发现:这种文具盒每个星期的销售量y(个)与它的定价 x(元/个)的关系如图所示:
(1)求这种文具盒每个星期的销售量 y(个)与它的定价 x(元/个)之间的函数关系式(不必写出自变量 x的取值范围);
(2)每个文具盒的定价是多少元,超市每星期销售这种文具盒 (不考虑其他因素)可或得的利润为 1200 元?
(3)若该超市每星期销售这种文具盒的销售量小于 115 个, 且单件利润不低于 4 元(x 为整数),当每个文具盒定价多少 元时,超市每星期利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
(1)求证:AC2=ADAB;
(2)求证:AC2+BC2=AB2(即证明勾股定理);
(3)如果AC=4,BC=9,求AD:DB的值;
(4)如果AD=4,DB=9,求AC:BC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=8,AD=6,折叠纸片使AD边与对角线BD重合,折痕为DG,则线段A'B的长度为____,折痕DG的长度为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
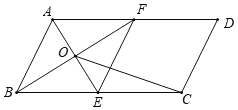
【题目】如图,在ABCD中,BC=2AB,点E、F分别是BC、AD的中点,AE、BF交于点O,连接EF,OC.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,∠ABC=60°,求OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个一次函数的图象与一个反比例函数的图象交于点![]() .
.
![]() 分别求出这两个函数的表达式;
分别求出这两个函数的表达式;
![]() 在同一个平面直角坐标系中画出这两个函数的图象,根据图象回答:当
在同一个平面直角坐标系中画出这两个函数的图象,根据图象回答:当![]() 取何值时,一次函数的值大于反比例函数的值?
取何值时,一次函数的值大于反比例函数的值?
![]() 求平面直角坐标中原点
求平面直角坐标中原点![]() 与
与![]() 点构成的三角形的面积.
点构成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书报亭开设两种租书方式:一种是零星租书,每册收费1元;另一种是会员卡租书,办卡费每月12元,租书费每册0.4元.小军经常来该店租书,若每月租书数量为x册.
(1)写出零星租书方式应付金额![]() (元)与租书数量x(册)之间的函数关系式。
(元)与租书数量x(册)之间的函数关系式。
(2)写出会员卡租书方式应付金额![]() (元)与租书数量x(册)之间的函数关系式.
(元)与租书数量x(册)之间的函数关系式.
(3)小军选取哪种租书方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家准备给边长为6m的正方形客厅用黑色和白色两种瓷砖铺设,如图所示:①黑色瓷砖区域Ⅰ:位于四个角的边长相同的小正方形及宽度相等的回字型边框(阴影部分),②白色瓷砖区域Ⅱ:四个全等的长方形及客厅中心的正方形(空白部分).设四个角上的小正方形的边长为x(m).

(1)当x=0.8时,若客厅中心的正方形瓷砖铺设的面积为16m2,求回字型黑色边框的宽度;
(2)若客厅中心的正方形边长为4m,白色瓷砖区域Ⅱ的总面积为26m2,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com