
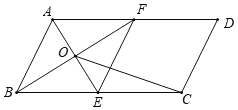
【题目】如图,在ABCD中,BC=2AB,点E、F分别是BC、AD的中点,AE、BF交于点O,连接EF,OC.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,∠ABC=60°,求OC的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)首先证明四边形ABEF是平行四边形,然后根据邻边相等的平行四边形是菱形即可证明;
(2)过点O作OG⊥BC于点G.分别在Rt△OEG,Rt△OCG中,由含30度角的直角三角形的性质和勾股定理解答即可.
(1)∵四边形ABCD是平行四边形,
∴BC∥AD,BC=AD.
∵E,F分别是BC,AD的中点,
∴BE![]() BC,AF
BC,AF![]() AD,
AD,
∴BE=AF,
∴四边形ABEF是平行四边形.
∵BC=2AB,
∴AB=BE,
∴平行四边形ABEF是菱形.
(2)过点O作OG⊥BC于点G,如图所示,
∵E是BC的中点,BC=2AB,
∴BE=CE=AB=4.
∵四边形ABEF是菱形,∠ABC=60°,
∴BE=CE=AB=4,∠OBE=30°,∠BOE=90°,
∴OE=2,∠OEB=60°,
∴GE=1,OG![]() GE
GE![]() ,
,
∴GC=GE+CE=5,
∴OC![]() 2
2![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
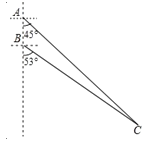
【题目】如图所示,我国两艘海监船 A,B 在南海海域巡逻,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船 C,此时,B 船在A 船的正南方向 15 海里处,A 船测得渔船 C 在其南偏东 45°方向,B 船测得渔船 C 在其南偏东 53°方向,已知 A 船的航速为 30 海里/小时,B 船的航速为 25 海里/小时,问 C 船至少要等待多长时间才能得到救援?(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈ 4 ,
,tan53°≈ 4 ,![]() 1.41 )
1.41 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《函数的图象与性质》拓展学习片段展示:
【问题】
如图①,在平面直角坐标系中,抛物线y=a(x-2)2-4经过原点O,与x轴的另一个交点为A,则a= ,点A的坐标为 .
【操作】
将图①中的抛物线在x轴下方的部分沿x轴翻折到x轴上方,如图②.直接写出翻折后的这部分抛物线对应的函数解析式: .
【探究】
在图②中,翻折后的这部分图象与原抛物线剩余部分的图象组成了一个“W”形状的新图象,则新图象对应的函数y随x的增大而增大时,x的取值范围是 .
【应用】结合上面的操作与探究,继续思考:
如图③,若抛物线y=(x-h)2-4与x轴交于A,B两点(A在B左),将抛物线在x轴下方的部分沿x轴翻折,同样,也得到了一个“W”形状的新图象.
(1)求A、B两点的坐标;(用含h的式子表示)
(2)当1<x<2时,若新图象的函数值y随x的增大而增大,求h的取值范围.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市初中学生每天进行体育锻炼的时间,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
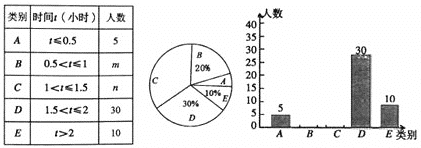
请根据图表信息解答下列问题:
(1)在统计表中,m=_______,n=____,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是_______;
(3)据了解该市大约有3万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值.
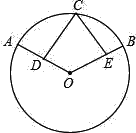
(2)如图:![]() =
=![]() ,D、E分别是半径OA和OB的中点.求证:CD=CE.
,D、E分别是半径OA和OB的中点.求证:CD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的三张形状相同、大小完全相同的方格纸,方格纸中每个小正方形的边长为1,请依次在3个图中画出满足要求的三角形,要求所画的三角形的各顶点必须与方格纸中小正方形的顶点重合.
(1)画一个底边长为4,面积为10的等腰三角形;
(2)画一个面积为10的等腰直角三角形;
(3)画一个一边长为2![]() 且面积为10的等腰三角形.
且面积为10的等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班开展了为期一周的“孝敬父母,帮做家务”社会活动,并根据学生帮家长做家务的时间来评价学生在活动中的表现,把结果划分成A,B,C,D,E五个等级.老师通过家长调查了全班50名学生在这次活动中帮父母做家务的时间,制作成如下的频数分布表和扇形统计图.
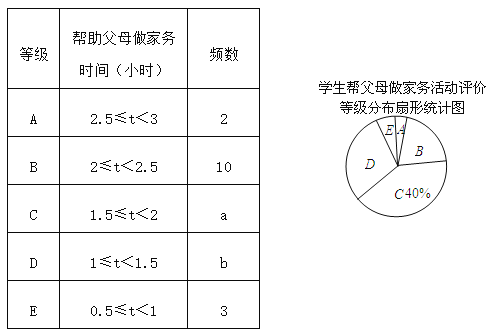
(1)求a,b的值;
(2)根据频数分布表估计该班学生在这次社会活动中帮父母做家务的平均时间;
(3)该班的小明同学这一周帮父母做家务2小时,他认为自己帮父母做家务的时间比班级里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计量说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一抛物线与x轴的交点是A(﹣2,0),B(1,0),且经过点C(2,8).
(1)求该抛物线的解析式,并写出顶点坐标.
(2)直接写出当y>8时,x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com