
【题目】已知一抛物线与x轴的交点是A(﹣2,0),B(1,0),且经过点C(2,8).
(1)求该抛物线的解析式,并写出顶点坐标.
(2)直接写出当y>8时,x的取值范围.
【答案】(1)(﹣![]() ,﹣
,﹣![]() );(2)当y>8时,x的取值范围是x<﹣3或x>2.
);(2)当y>8时,x的取值范围是x<﹣3或x>2.
【解析】
(1)设交点式y=a(x+2)(x-1),然后把C点坐标代入求出a的值即可得到抛物线解析式,把解析式配成顶点式即可得到抛物线顶点坐标;
(2)先求出点C(2,8)关于对称轴x=-![]() 的对称点为(-3,8),再根据二次函数的性质即可求解.
的对称点为(-3,8),再根据二次函数的性质即可求解.
(1)折抛物线解析式为y=a(x+2)(x﹣1),
把C(2,8)代入得a41=8,解得a=2,
所以抛物线解析式为y=2(x+2)(x﹣1),
即y=2x2+2x﹣4=2x2+2x﹣4=2(x+![]() )2﹣
)2﹣![]() ,
,
所以抛物线的顶点坐标为(﹣![]() ,﹣
,﹣![]() );
);
(2)∵y=2x2+2x﹣4=2(x+![]() )2﹣
)2﹣![]() ,
,
∴对称轴是直线x=﹣![]() a=2>0开口向上,
a=2>0开口向上,
∴点C(2,8)关于对称轴的对称点为(﹣3,8),
∴当y>8时,x的取值范围是x<﹣3或x>2.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
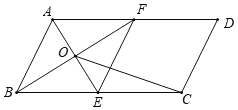
【题目】如图,在ABCD中,BC=2AB,点E、F分别是BC、AD的中点,AE、BF交于点O,连接EF,OC.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,∠ABC=60°,求OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△ABC中,AB=AC,∠A=36°,D是AC上的一点,AD=BD,则以下结论中正确的有( )
①△BCD是等腰三角形;②点D是线段AC的黄金分割点;③△BCD∽△ABC;④BD平分∠ABC.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
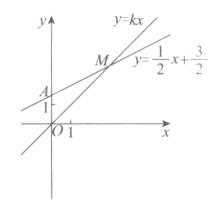
【题目】如图,直线![]() 与y轴的交点为A,直线
与y轴的交点为A,直线![]() 与直线
与直线![]() 的交点M的坐标为
的交点M的坐标为![]() .
.
(1)求a和k的值;
(2)直接写出关于x的不等式![]() 的解集;
的解集;
(3)若点B在x轴上,![]() ,直接写出点B的坐标.
,直接写出点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,连接
边上,连接![]() ,连接
,连接![]()
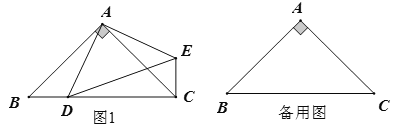
(1)求证:![]()
(2)点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]()
①补全图形并证明![]()
②利用备用图进行画图、试验、探究,找出当![]() 三点恰好共线时点
三点恰好共线时点![]() 的位置,请直接写出此时
的位置,请直接写出此时![]() 的度数,并画出相应的图形
的度数,并画出相应的图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家准备给边长为6m的正方形客厅用黑色和白色两种瓷砖铺设,如图所示:①黑色瓷砖区域Ⅰ:位于四个角的边长相同的小正方形及宽度相等的回字型边框(阴影部分),②白色瓷砖区域Ⅱ:四个全等的长方形及客厅中心的正方形(空白部分).设四个角上的小正方形的边长为x(m).

(1)当x=0.8时,若客厅中心的正方形瓷砖铺设的面积为16m2,求回字型黑色边框的宽度;
(2)若客厅中心的正方形边长为4m,白色瓷砖区域Ⅱ的总面积为26m2,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,AE、BF 是角平分线,交于 O 点.
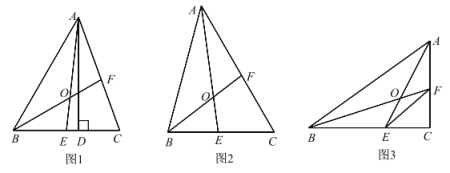
(1)如图 1,AD 是高,∠BAC=90°,∠C=70°,求∠DAC 和∠BOA 的度数;
(2)如图 2,若 OE=OF,求∠C 的度数;
(3)如图 3,若∠C=90°,BC=8,AC=6,S△CEF=4,求 S△AOB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为( )(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
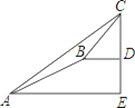
A. 8.1米 B. 17.2米 C. 19.7米 D. 25.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现场学习题:
问题背景:
在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积.
,求这个三角形的面积.
小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.
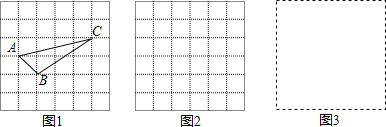
(1)请你将△ABC的面积直接填写在横线上. .
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法,若△ABC三边的长分别为![]() a,2
a,2![]() a、
a、![]() a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是: .
a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是: .
探索创新:
(3)若△ABC三边的长分别为![]() 、
、![]() 、
、![]() (m>0,n>0,m≠n),请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为: .
(m>0,n>0,m≠n),请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com