
【题目】如图1,在等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,连接
边上,连接![]() ,连接
,连接![]()
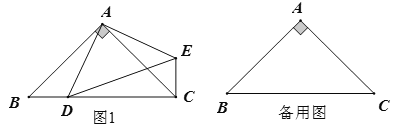
(1)求证:![]()
(2)点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]()
①补全图形并证明![]()
②利用备用图进行画图、试验、探究,找出当![]() 三点恰好共线时点
三点恰好共线时点![]() 的位置,请直接写出此时
的位置,请直接写出此时![]() 的度数,并画出相应的图形
的度数,并画出相应的图形
【答案】(1)证明见解析;(2)①见解析;②画图见解析,![]() .
.
【解析】
(1)先根据同角的余角相等推出∠BAD=∠CAE,再根据SAS证得△BAD≌△CAE,进而可得结论;
(2)①根据题意作图即可补全图形;利用轴对称的性质可得ME=AE,CM=CA,然后根据SSS可推出△CME≌△CAE,再利用全等三角形的性质和(1)题的∠BAD=∠CAE即可证得结论;
②当![]() 三点恰好共线时,设AC、DM交于点H,如图3,由前面两题的结论和等腰直角三角形的性质可求得∠DCM=135°,然后在△AEH和△DCH中利用三角形的内角和可得∠HAE=∠HDC,进而可得
三点恰好共线时,设AC、DM交于点H,如图3,由前面两题的结论和等腰直角三角形的性质可求得∠DCM=135°,然后在△AEH和△DCH中利用三角形的内角和可得∠HAE=∠HDC,进而可得![]() ,接着在△CDM中利用三角形的内角和定理求出∠CMD的度数,再利用①的结论即得答案.
,接着在△CDM中利用三角形的内角和定理求出∠CMD的度数,再利用①的结论即得答案.
解:(1)证明:∵AE⊥AD,∴∠DAE=90°,∴∠CAE+∠DAC=90°,
∵∠BAC=90°,∴∠BAD+∠DAC=90°,
∴∠BAD=∠CAE,
又∵BA=CA,DA=EA,
∴△BAD≌△CAE(SAS),
∴![]() ;
;
(2)①补全图形如图2所示,∵点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,∴ME=AE,CM=CA,
,∴ME=AE,CM=CA,
∵CE=CE,∴△CME≌△CAE(SSS),
∴![]() ,
,
∵∠BAD=∠CAE,
∴![]() ;
;
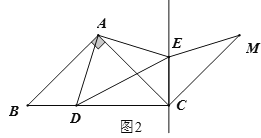
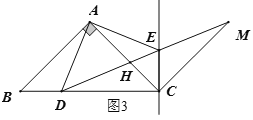
②当![]() 三点恰好共线时,设AC、DM交于点H,如图3,由(1)题知:
三点恰好共线时,设AC、DM交于点H,如图3,由(1)题知:![]() ,
,
∵△CME≌△CAE,∴![]() ,∴∠DCM=135°,
,∴∠DCM=135°,
在△AEH和△DCH中,∵∠AEH=∠ACD=45°,∠AHE=∠DHC,∴∠HAE=∠HDC,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】(1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值.
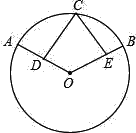
(2)如图:![]() =
=![]() ,D、E分别是半径OA和OB的中点.求证:CD=CE.
,D、E分别是半径OA和OB的中点.求证:CD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=x-5,令x=![]() ,1,
,1,![]() ,2,
,2,![]() ,3,
,3,![]() ,4,
,4,![]() ,5,可得函数图象上的十个点.在这十个点中随机取两个点P(x1,y1),Q(x2,y2),则P,Q两点在同一反比例函数图象上的概率是( )
,5,可得函数图象上的十个点.在这十个点中随机取两个点P(x1,y1),Q(x2,y2),则P,Q两点在同一反比例函数图象上的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
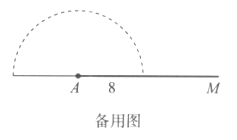
【题目】程老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题,操作学具时,点Q在轨道槽AM上运动,点P既能在以A为圆心、以8为半径的半圆轨道槽上运动,也能在轨道槽QN上运动,图2是操作学具时,所对应某个位置的图形的示意图.

有以下结论:
①当∠PAQ=30°,PQ=6时,可得到形状唯一确定的△PAQ
②当∠PAQ=30°,PQ=9时,可得到形状唯一确定的△PAQ
③当∠PAQ=90°,PQ=10时,可得到形状唯一确定的△PAQ
④当∠PAQ=150°,PQ=12时,可得到形状唯一确定的△PAQ
其中所有正确结论的序号是( )
A.②③B.③④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
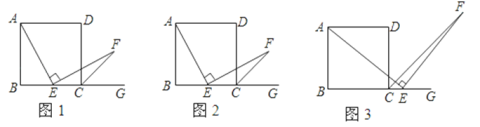
如图,在正方形ABCD中,点E是线段BG上的动点,AE⊥EF,EF交正方形外角∠DCG的平分线CF于点F.
(探究展示)
(1)如图1,若点E是BC的中点,证明:∠BAE+∠EFC=∠DCF.
(2)如图2,若点E是BC的上的任意一点(B、C除外),∠BAE+∠EFC=∠DCF是否仍然成立?若成立,请予以证明;若不成立,请说明理由.
(拓展延伸)
(3)如图3,若点E是BC延长线(C除外)上的任意一点,求证:AE=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一抛物线与x轴的交点是A(﹣2,0),B(1,0),且经过点C(2,8).
(1)求该抛物线的解析式,并写出顶点坐标.
(2)直接写出当y>8时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△AOB是直角三角形,∠AOB=90°,边AB与y轴交于点C.

(1)若∠A=∠AOC,试说明:∠B=∠BOC;
(2)延长AB交x轴于点E,过O作OD⊥AB,若∠DOB=∠EOB,∠A=∠E,求∠A的度数;
(3)如图,OF平分∠AOM,∠BCO的平分线交FO的延长线于点P,∠A=40°,当△ABO绕O点旋转时(边AB与y轴正半轴始终相交于点C),问∠P的度数是否发生改变?若不变,求其度数;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
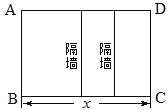
【题目】某工厂拟建一座平面图形为矩形且面积为200平方米的三级污水处理池(平面图如图ABCD所示).由于地形限制,三级污水处理池的长、宽都不能超过16米.如果池的外围墙建造单价为每米400元,中间两条隔墙建造单价为每米300元,池底建造单价为每平方米80元.(池墙的厚度忽略不计)当三级污水处理池的总造价为47200元时,求池长x.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com