
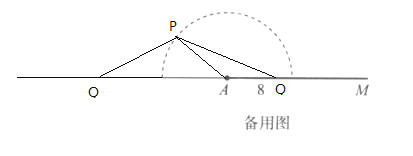
【题目】程老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题,操作学具时,点Q在轨道槽AM上运动,点P既能在以A为圆心、以8为半径的半圆轨道槽上运动,也能在轨道槽QN上运动,图2是操作学具时,所对应某个位置的图形的示意图.

有以下结论:
①当∠PAQ=30°,PQ=6时,可得到形状唯一确定的△PAQ
②当∠PAQ=30°,PQ=9时,可得到形状唯一确定的△PAQ
③当∠PAQ=90°,PQ=10时,可得到形状唯一确定的△PAQ
④当∠PAQ=150°,PQ=12时,可得到形状唯一确定的△PAQ
其中所有正确结论的序号是( )
A.②③B.③④C.②③④D.①②③④
【答案】C
【解析】
分别在以上四种情况下以P为圆心,PQ的长度为半径画弧,观察弧与直线AM的交点即为Q点,作出![]() 后可得答案.
后可得答案.
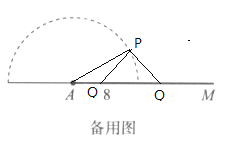
如下图,当∠PAQ=30°,PQ=6时,以P为圆心,PQ的长度为半径画弧,弧与直线AM有两个交点,作出![]() ,发现两个位置的Q都符合题意,所以
,发现两个位置的Q都符合题意,所以![]() 不唯一,所以①错误.
不唯一,所以①错误.
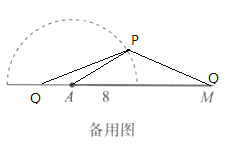
如下图,当∠PAQ=30°,PQ=9时,以P为圆心,PQ的长度为半径画弧,弧与直线AM有两个交点,作出![]() ,发现左边位置的Q不符合题意,所以
,发现左边位置的Q不符合题意,所以![]() 唯一,所以②正确.
唯一,所以②正确.
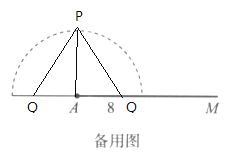
如下图,当∠PAQ=90°,PQ=10时,以P为圆心,PQ的长度为半径画弧,弧与直线AM有两个交点,作出![]() ,发现两个位置的Q都符合题意,但是此时两个三角形全等,所以形状相同,所以
,发现两个位置的Q都符合题意,但是此时两个三角形全等,所以形状相同,所以![]() 唯一,所以③正确.
唯一,所以③正确.
如下图,当∠PAQ=150°,PQ=12时,以P为圆心,PQ的长度为半径画弧,弧与直线AM有两个交点,作出![]() ,发现左边位置的Q不符合题意,所以
,发现左边位置的Q不符合题意,所以![]() 唯一,所以④正确.
唯一,所以④正确.
综上:②③④正确.
故选C.


科目:初中数学 来源: 题型:
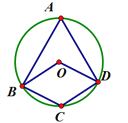
【题目】四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合)。若四边形OBCD是平行四边形时,那么![]() 的数量关系是________________.
的数量关系是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△ABC中,AB=AC,∠A=36°,D是AC上的一点,AD=BD,则以下结论中正确的有( )
①△BCD是等腰三角形;②点D是线段AC的黄金分割点;③△BCD∽△ABC;④BD平分∠ABC.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
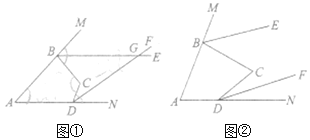
【题目】如图①,![]() 、
、![]() 分别平分四边形
分别平分四边形![]() 的外角
的外角![]() 和
和![]() ,设
,设![]() ,
,![]() .
.
(1)若![]() ,则
,则![]()
![]() ;
;
(2)若![]() 与
与![]() 相交于点
相交于点![]() ,且
,且![]() ,求
,求![]() 、
、![]() 所满足的等量关系式,并说明理由;
所满足的等量关系式,并说明理由;
(3)如图②,若![]() ,试判断
,试判断![]() 、
、![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
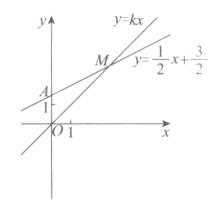
【题目】如图,直线![]() 与y轴的交点为A,直线
与y轴的交点为A,直线![]() 与直线
与直线![]() 的交点M的坐标为
的交点M的坐标为![]() .
.
(1)求a和k的值;
(2)直接写出关于x的不等式![]() 的解集;
的解集;
(3)若点B在x轴上,![]() ,直接写出点B的坐标.
,直接写出点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,连接
边上,连接![]() ,连接
,连接![]()
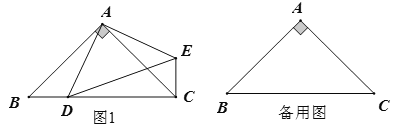
(1)求证:![]()
(2)点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]()
①补全图形并证明![]()
②利用备用图进行画图、试验、探究,找出当![]() 三点恰好共线时点
三点恰好共线时点![]() 的位置,请直接写出此时
的位置,请直接写出此时![]() 的度数,并画出相应的图形
的度数,并画出相应的图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,AE、BF 是角平分线,交于 O 点.
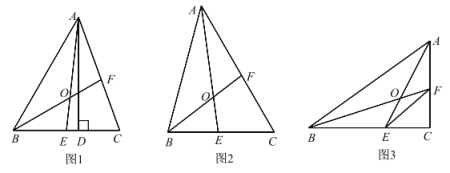
(1)如图 1,AD 是高,∠BAC=90°,∠C=70°,求∠DAC 和∠BOA 的度数;
(2)如图 2,若 OE=OF,求∠C 的度数;
(3)如图 3,若∠C=90°,BC=8,AC=6,S△CEF=4,求 S△AOB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com