
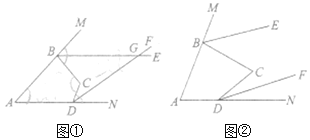
【题目】如图①,![]() 、
、![]() 分别平分四边形
分别平分四边形![]() 的外角
的外角![]() 和
和![]() ,设
,设![]() ,
,![]() .
.
(1)若![]() ,则
,则![]()
![]() ;
;
(2)若![]() 与
与![]() 相交于点
相交于点![]() ,且
,且![]() ,求
,求![]() 、
、![]() 所满足的等量关系式,并说明理由;
所满足的等量关系式,并说明理由;
(3)如图②,若![]() ,试判断
,试判断![]() 、
、![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
【答案】(1)110;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() ,理由见解析
,理由见解析
【解析】
(1)根据四边形的内角和与邻补角的性质即可求解;
(2)连接BD,先得到![]() ,再根据三角形的内角和得到角度的关系即可求解;
,再根据三角形的内角和得到角度的关系即可求解;
(3)由(1)有,∠MBC+∠NDC=![]() ,BE、DF分别平分四边形的外角∠MBC和∠NDC,则∠CBE+∠CDH=
,BE、DF分别平分四边形的外角∠MBC和∠NDC,则∠CBE+∠CDH=![]() (
(![]() ),∠CBE+β∠DHB=
),∠CBE+β∠DHB=![]() (
(![]() ),根据
),根据![]() =
=![]() ,则有∠CBE+
,则有∠CBE+![]() ∠DHB=
∠DHB=![]() (
(![]() +
+![]() )=
)=![]() ,得到∠CBE=∠DHB,故可得到BE∥DF.
,得到∠CBE=∠DHB,故可得到BE∥DF.
解:(1)∵∠ABC+∠ADC=360°(![]() )=250°,
)=250°,
∴∠MBC+∠NDC=180°∠ABC+180°∠ADC=360°-(∠ABC+∠ADC)=![]() =110°.
=110°.
故答案为:110;
(2)![]() .理由如下:如解图①,连接BD,
.理由如下:如解图①,连接BD,
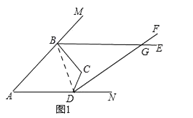
由(1)知,![]() ,
,
![]() 、
、![]() 分别平分四边形
分别平分四边形![]() 的外角
的外角![]() 和
和![]() ,
,
∴![]() ,
,![]()
![]() .
.
在△BCD中,∠BDC+∠CBD=180°∠BCD=180°![]() ,
,
在△BDG中,∠GBD+∠GDB+∠BGD=180°,
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,
∴(∠CBG+∠CDG)+(∠BDC+∠CBD)+∠BGD=180°,
∴![]() (
(![]() )+180°
)+180°![]() +25°=180°,
+25°=180°,
整理得![]() ;
;
(3)![]() .理由如下,如解图②所示,延长
.理由如下,如解图②所示,延长![]() 交
交![]() 于点
于点![]() ,
,

由(1)、(2)可知,![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
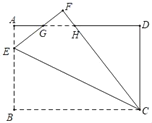
【题目】如图,长方形纸片ABCD中,AB=4,BC=6,点E在AB边上,将纸片沿CE折叠,点B落在点F处,EF,CF分别交AD于点G,H,且EG=GH,则AE的长为( )
A. ![]() B. 1C.
B. 1C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个矩形ABCD的较短边长为2.
(1)如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;
(2)如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=x-5,令x=![]() ,1,
,1,![]() ,2,
,2,![]() ,3,
,3,![]() ,4,
,4,![]() ,5,可得函数图象上的十个点.在这十个点中随机取两个点P(x1,y1),Q(x2,y2),则P,Q两点在同一反比例函数图象上的概率是( )
,5,可得函数图象上的十个点.在这十个点中随机取两个点P(x1,y1),Q(x2,y2),则P,Q两点在同一反比例函数图象上的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
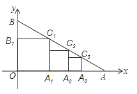
【题目】如图,在平面直角坐标系中,点A(![]() ,0),点B(0,1),作第一个正方形OA1C1B1且点A1在OA上,点B1在OB上,点C1在AB上;作第二个正方形A1A2C2B2且点A2在A1A上,点B2在A1C2上,点C2在AB上…,如此下去,则点Cn的纵坐标为________.
,0),点B(0,1),作第一个正方形OA1C1B1且点A1在OA上,点B1在OB上,点C1在AB上;作第二个正方形A1A2C2B2且点A2在A1A上,点B2在A1C2上,点C2在AB上…,如此下去,则点Cn的纵坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题,操作学具时,点Q在轨道槽AM上运动,点P既能在以A为圆心、以8为半径的半圆轨道槽上运动,也能在轨道槽QN上运动,图2是操作学具时,所对应某个位置的图形的示意图.

有以下结论:
①当∠PAQ=30°,PQ=6时,可得到形状唯一确定的△PAQ
②当∠PAQ=30°,PQ=9时,可得到形状唯一确定的△PAQ
③当∠PAQ=90°,PQ=10时,可得到形状唯一确定的△PAQ
④当∠PAQ=150°,PQ=12时,可得到形状唯一确定的△PAQ
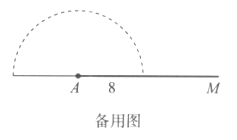
其中所有正确结论的序号是( )
A.②③B.③④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
如图,在正方形ABCD中,点E是线段BG上的动点,AE⊥EF,EF交正方形外角∠DCG的平分线CF于点F.
(探究展示)
(1)如图1,若点E是BC的中点,证明:∠BAE+∠EFC=∠DCF.
(2)如图2,若点E是BC的上的任意一点(B、C除外),∠BAE+∠EFC=∠DCF是否仍然成立?若成立,请予以证明;若不成立,请说明理由.
(拓展延伸)
(3)如图3,若点E是BC延长线(C除外)上的任意一点,求证:AE=EF.
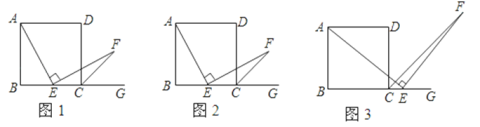
查看答案和解析>>
科目:初中数学 来源: 题型:
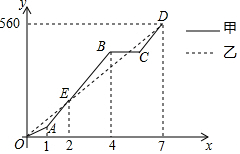
【题目】端午节期间,甲、乙两人沿同一路线行驶,各自开车同时去离家560千米的景区游玩,甲先以每小时60千米的速度匀速行驶1小时,再以每小时m千米的速度匀速行驶,途中体息了一段时间后,仍按照每小时m千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程![]() ,
,![]() 与时间
与时间![]() 之间的函数关系的图象
之间的函数关系的图象![]() 请根据图象提供的信息,解决下列问题:
请根据图象提供的信息,解决下列问题:
![]() 图中E点的坐标是______,题中
图中E点的坐标是______,题中![]() ______
______![]() ,甲在途中休息______h;
,甲在途中休息______h;
![]() 求线段CD的解析式,并写出自变量x的取值范围;
求线段CD的解析式,并写出自变量x的取值范围;
![]() 两人第二次相遇后,又经过多长时间两人相距20km?
两人第二次相遇后,又经过多长时间两人相距20km?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com