
【题目】(问题情境)
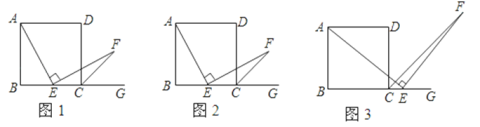
如图,在正方形ABCD中,点E是线段BG上的动点,AE⊥EF,EF交正方形外角∠DCG的平分线CF于点F.
(探究展示)
(1)如图1,若点E是BC的中点,证明:∠BAE+∠EFC=∠DCF.
(2)如图2,若点E是BC的上的任意一点(B、C除外),∠BAE+∠EFC=∠DCF是否仍然成立?若成立,请予以证明;若不成立,请说明理由.
(拓展延伸)
(3)如图3,若点E是BC延长线(C除外)上的任意一点,求证:AE=EF.
【答案】(1)证明见解析;(2)成立;证明见解析;(3)证明见解析.
【解析】
(1)取AB的中点M,连结EM,根据正方形的性质和全等三角形的判定证明即可;
(2)在AB上取一点M,使AM=CE,连接ME,根据已知条件利用ASA判定![]() ,利用全等三角形的性质证明即可.
,利用全等三角形的性质证明即可.
(3)在BA的延长线上取一点M,使AM=CE,连接ME,根据已知利用ASA判定![]() ,利用全等三角形的性质证明即可.
,利用全等三角形的性质证明即可.
(1)证明:取AB的中点M,连结EM,如图1:
∵M是AB的中点,E是BC的中点,
∴在正方形ABCD中,AM=EC,
∵CF是∠DCG的平分线,
∴∠BCF=135°,
∴∠AME=∠ECF=135°,
∵∠MAE=∠CEF=45°,
在△AME与△ECF中,
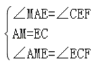 ,
,
∴△AME≌△ECF(SAS),
∴∠BAE+∠EFC=∠FCG=∠DCF;
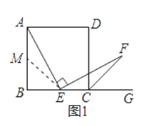
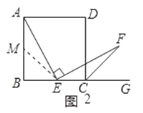
(2)证明:取AB上的任意一点使得AM=EC,连结EM,如图2:
∵AE⊥EF,AB⊥BC,
∴∠BAE+∠BEA=90°,∠BEA+∠CEF=90°,
∴∠MAE=∠CEF,
∵AM=EC,
∴在正方形ABCD中,BM=BE,
∴∠AME=∠ECF=135°,
在△AME与△ECF中,
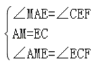 ,
,
∴△AME≌△ECF(SAS),
∴∠BAE+∠EFC=∠FCG=∠DCF;
(3)证明:取AB延长线上的一点M使得AM=CE,如图3:
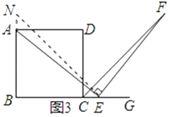
∵AM=CE,AB⊥BC,
∴∠AME=45°,
∴∠ECF=AME=45°,
∵AD∥BE,
∴∠DAE=∠BEA,
∵MA⊥AD,AE⊥EF,
∴∠MAE=∠CEF,
在△AME与△ECF中,
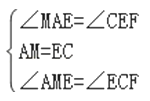 ,
,
∴△AME≌△ECF(SAS),
∴AE=EF.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
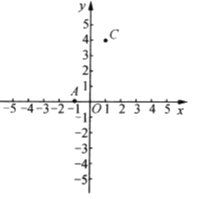
【题目】如图,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,且
轴上,且![]() .
.
(1)求点![]() 的坐标,并画出
的坐标,并画出![]() ;
;
(2)求![]() 的面积;
的面积;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 三点为顶点的三角形的面积为10?若存在,请直接写出点
三点为顶点的三角形的面积为10?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
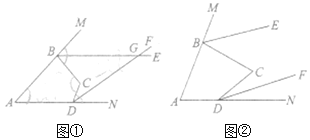
【题目】如图①,![]() 、
、![]() 分别平分四边形
分别平分四边形![]() 的外角
的外角![]() 和
和![]() ,设
,设![]() ,
,![]() .
.
(1)若![]() ,则
,则![]()
![]() ;
;
(2)若![]() 与
与![]() 相交于点
相交于点![]() ,且
,且![]() ,求
,求![]() 、
、![]() 所满足的等量关系式,并说明理由;
所满足的等量关系式,并说明理由;
(3)如图②,若![]() ,试判断
,试判断![]() 、
、![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=30°,∠ACB=45°,BD∥AC,BD=AB,且C,D两点位于AB所在直线两侧,射线AD上的点E满足∠ABE=60°.
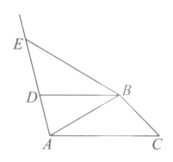
(1)∠AEB=___________°;
(2)图中与AC相等的线段是_____________,证明此结论只需证明△________≌△_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,连接
边上,连接![]() ,连接
,连接![]()
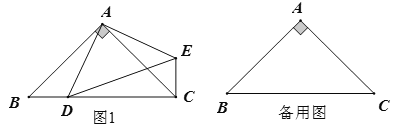
(1)求证:![]()
(2)点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]()
①补全图形并证明![]()
②利用备用图进行画图、试验、探究,找出当![]() 三点恰好共线时点
三点恰好共线时点![]() 的位置,请直接写出此时
的位置,请直接写出此时![]() 的度数,并画出相应的图形
的度数,并画出相应的图形
查看答案和解析>>
科目:初中数学 来源: 题型:
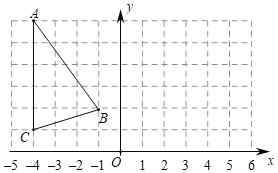
【题目】如图,平面直角坐标系xoy中A(﹣4,6),B(﹣1,2),C(﹣4,1).
(1)作出△ABC关于直线x=1对称的图形△A1B1C1并写出△A1B1C1各顶点的坐标;
(2)将△A1B1C1向左平移2个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△ABC和△A2B2C2,它们是否关于某直线对称?若是,请指出对称轴,并求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 是
是![]() 轴正半轴的一个动点,过点
轴正半轴的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交双曲线
交双曲线![]() 于点
于点![]() ,连接
,连接![]() .
.
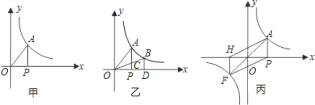
![]() 如图甲,当点
如图甲,当点![]() 在
在![]() 轴的正方向上运动时,
轴的正方向上运动时,![]() 的面积大小是否变化?若不变,请求出
的面积大小是否变化?若不变,请求出![]() 的面积;若改变,试说明理由;
的面积;若改变,试说明理由;
![]() 如图乙,在
如图乙,在![]() 轴上的点
轴上的点![]() 的右侧有一点
的右侧有一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线交双曲线于点
轴的垂线交双曲线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,设
,设![]() 的面积是
的面积是![]() ,梯形
,梯形![]() 的面积为
的面积为![]() ,写出
,写出![]() 与
与![]() 的大小关系(用 “
的大小关系(用 “![]() ”、“
”、“![]() ”、“
”、“![]() ”表示);
”表示);
![]() 如图丙,
如图丙,![]() 的延长线与双曲线
的延长线与双曲线![]() 的另一个交点为
的另一个交点为![]() ,
,![]() 垂直于
垂直于![]() 轴,垂足为点
轴,垂足为点![]() ,连接
,连接![]() ,
,![]() ,试证明四边形
,试证明四边形![]() 的面积为一个常数.
的面积为一个常数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com