
【题目】点![]() 是
是![]() 轴正半轴的一个动点,过点
轴正半轴的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交双曲线
交双曲线![]() 于点
于点![]() ,连接
,连接![]() .
.
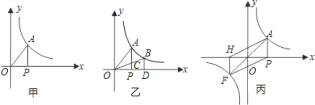
![]() 如图甲,当点
如图甲,当点![]() 在
在![]() 轴的正方向上运动时,
轴的正方向上运动时,![]() 的面积大小是否变化?若不变,请求出
的面积大小是否变化?若不变,请求出![]() 的面积;若改变,试说明理由;
的面积;若改变,试说明理由;
![]() 如图乙,在
如图乙,在![]() 轴上的点
轴上的点![]() 的右侧有一点
的右侧有一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线交双曲线于点
轴的垂线交双曲线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,设
,设![]() 的面积是
的面积是![]() ,梯形
,梯形![]() 的面积为
的面积为![]() ,写出
,写出![]() 与
与![]() 的大小关系(用 “
的大小关系(用 “![]() ”、“
”、“![]() ”、“
”、“![]() ”表示);
”表示);
![]() 如图丙,
如图丙,![]() 的延长线与双曲线
的延长线与双曲线![]() 的另一个交点为
的另一个交点为![]() ,
,![]() 垂直于
垂直于![]() 轴,垂足为点
轴,垂足为点![]() ,连接
,连接![]() ,
,![]() ,试证明四边形
,试证明四边形![]() 的面积为一个常数.
的面积为一个常数.
【答案】(1)![]() 的面积不变,
的面积不变,![]() ;
; ![]() ;
; ![]() 四边形
四边形![]() 的面积是
的面积是![]() .
.
【解析】
(1)本题还可依据比例系数k的几何意义,得出两个三角形的面积都等于![]() ,因而当点P在x轴的正方向上运动时,Rt△AOP的面积大小不变;
,因而当点P在x轴的正方向上运动时,Rt△AOP的面积大小不变;
(2)根据(1)可以得到△BDO的面积,因而S1>S2;
(3)设A的坐标是(a,b),根据反比例函数是中心对称图形,因而F点的坐标是(-a,-b),则AP=b,HP=2a,则四边形APFH的面积是2ab,从而得到四边形APFH的面积是2.
(1)![]() 的面积不变,
的面积不变,![]() ;
;
![]() 根据
根据![]() 的面积等于
的面积等于![]() ,
,![]() 的面积大于
的面积大于![]() ,
,![]() ;
;
![]() 设
设![]() 的坐标是
的坐标是![]() ,根据反比例函数是中心对称图形,因而
,根据反比例函数是中心对称图形,因而![]() 点的坐标是
点的坐标是![]() ,则
,则![]() ,
,![]() ,则四边形
,则四边形![]() 的面积是
的面积是![]() ,据
,据![]() 在双曲线
在双曲线![]() 的图象上,因而
的图象上,因而![]() ,则四边形
,则四边形![]() 的面积是
的面积是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(问题情境)
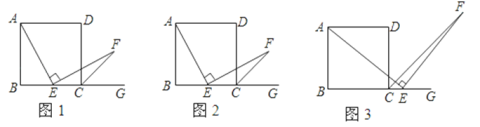
如图,在正方形ABCD中,点E是线段BG上的动点,AE⊥EF,EF交正方形外角∠DCG的平分线CF于点F.
(探究展示)
(1)如图1,若点E是BC的中点,证明:∠BAE+∠EFC=∠DCF.
(2)如图2,若点E是BC的上的任意一点(B、C除外),∠BAE+∠EFC=∠DCF是否仍然成立?若成立,请予以证明;若不成立,请说明理由.
(拓展延伸)
(3)如图3,若点E是BC延长线(C除外)上的任意一点,求证:AE=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=![]() 的图象如图所示,则以下结论:①m<0;②在每个分支上y随x的增大而增大;③若点A(-1,a),点B(2,b)在图象上,则a <b;④若点P(x,y)在图象上,则点P1(-x,y)也在图象上.其中正确的个数为( )
的图象如图所示,则以下结论:①m<0;②在每个分支上y随x的增大而增大;③若点A(-1,a),点B(2,b)在图象上,则a <b;④若点P(x,y)在图象上,则点P1(-x,y)也在图象上.其中正确的个数为( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
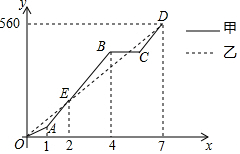
【题目】端午节期间,甲、乙两人沿同一路线行驶,各自开车同时去离家560千米的景区游玩,甲先以每小时60千米的速度匀速行驶1小时,再以每小时m千米的速度匀速行驶,途中体息了一段时间后,仍按照每小时m千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程![]() ,
,![]() 与时间
与时间![]() 之间的函数关系的图象
之间的函数关系的图象![]() 请根据图象提供的信息,解决下列问题:
请根据图象提供的信息,解决下列问题:
![]() 图中E点的坐标是______,题中
图中E点的坐标是______,题中![]() ______
______![]() ,甲在途中休息______h;
,甲在途中休息______h;
![]() 求线段CD的解析式,并写出自变量x的取值范围;
求线段CD的解析式,并写出自变量x的取值范围;
![]() 两人第二次相遇后,又经过多长时间两人相距20km?
两人第二次相遇后,又经过多长时间两人相距20km?
查看答案和解析>>
科目:初中数学 来源: 题型:
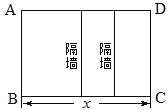
【题目】某工厂拟建一座平面图形为矩形且面积为200平方米的三级污水处理池(平面图如图ABCD所示).由于地形限制,三级污水处理池的长、宽都不能超过16米.如果池的外围墙建造单价为每米400元,中间两条隔墙建造单价为每米300元,池底建造单价为每平方米80元.(池墙的厚度忽略不计)当三级污水处理池的总造价为47200元时,求池长x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A城气象台测得台风中心在A城正西方向240km的O处,以每小时40km的速度向南偏东60°的OB方向移动,距台风中心130km的范围内是受台风影响的区域.
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到台风的影响,求出受台风影响的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲招聘一名部门经理,对甲、乙、丙三名候选人进行了笔试与面试,甲、乙、丙三人的笔试成绩分别为95分、94分和94分.他们的面试成绩如表:
候选人 | 评委1 | 评委2 | 评委3 |
甲 | 94 | 89 | 90 |
乙 | 92 | 90 | 94 |
丙 | 91 | 88 | 94 |
(1)分别求出甲、乙、丙三人的面试成绩的平均分![]() 、
、![]() 、和
、和![]() ;
;
(2)若按笔试成绩的40%与面试成绩的60%的和作为综合成绩,综合成绩高者将被录用,请你通过计算判断谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.一个事件发生的机会是99.99%,所以我们说这个事件必然会发生
B.抛一枚硬币,出现正面朝上的机会是![]() ,所以连续抛2次,则必定有一次正面朝上
,所以连续抛2次,则必定有一次正面朝上
C.甲、乙两人掷一枚正六面体骰子做游戏,规则是:出现1点时甲赢,出现2点时乙赢,出现其它点数时大家不分输赢,这个游戏对两人来说是公平的
D.在牌面是1~9的九张牌中随机地抽出一张,抽到牌面是奇数和偶数的机会是一样的
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com