
ΓΨΧβΡΩΓΩΡ≥ΙΪΥΨ”ϊ’–ΤΗ“ΜΟϊ≤ΩΟ≈Ψ≠άμΘ§Ε‘ΦΉΓΔ““ΓΔ±ϊ»ΐΟϊΚρ―Γ»ΥΫχ––ΝΥ± ‘”κΟφ ‘Θ§ΦΉΓΔ““ΓΔ±ϊ»ΐ»ΥΒΡ± ‘≥…Φ®Ζ÷±πΈΣ95Ζ÷ΓΔ94Ζ÷ΚΆ94Ζ÷Θ°ΥϊΟ«ΒΡΟφ ‘≥…Φ®»γ±μΘΚ
Κρ―Γ»Υ | ΤάΈ·1 | ΤάΈ·2 | ΤάΈ·3 |
ΦΉ | 94 | 89 | 90 |
““ | 92 | 90 | 94 |
±ϊ | 91 | 88 | 94 |
Θ®1Θ©Ζ÷±π«σ≥ωΦΉΓΔ““ΓΔ±ϊ»ΐ»ΥΒΡΟφ ‘≥…Φ®ΒΡΤΫΨυΖ÷![]() ΓΔ
ΓΔ![]() ΓΔΚΆ
ΓΔΚΆ![]() ΘΜ
ΘΜ
Θ®2Θ©»τΑ¥± ‘≥…Φ®ΒΡ40%”κΟφ ‘≥…Φ®ΒΡ60%ΒΡΚΆΉςΈΣΉέΚœ≥…Φ®Θ§ΉέΚœ≥…Φ®ΗΏ’ΏΫΪ±Μ¬Φ”ΟΘ§«κΡψΆ®ΙΐΦΤΥψ≈–ΕœΥ≠ΫΪ±Μ¬Φ”ΟΘ°
ΓΨ¥πΑΗΓΩΘΚ(1)![]() =91Ζ÷Θ§
=91Ζ÷Θ§![]() =92Ζ÷Θ§
=92Ζ÷Θ§![]() =91Ζ÷ΘΜ(2)““ΫΪ±Μ¬Φ”Ο.
=91Ζ÷ΘΜ(2)““ΫΪ±Μ¬Φ”Ο.
ΓΨΫβΈωΓΩ
(1)ΗυΨίΥψ θΤΫΨυ ΐΒΡΚ§“εΚΆ«σΖ®Θ§Ζ÷±π”Ο»ΐ»ΥΒΡΟφ ‘ΒΡΉή≥…Φ®≥ΐ“‘3Θ§«σ≥ωΦΉΓΔ““ΓΔ±ϊ»ΐ»ΥΒΡΟφ ‘ΒΡΤΫΨυΖ÷![]() ΓΔ
ΓΔ![]() ΚΆ
ΚΆ![]() Φ¥Ω…ΘΜ
Φ¥Ω…ΘΜ
(2) Ήœ»ΗυΨίΦ”»®ΤΫΨυ ΐΒΡΚ§“εΚΆ«σΖ®Θ§Ζ÷±π«σ≥ω»ΐ»ΥΒΡΉέΚœ≥…Φ®Ης «Εύ…ΌΘΜ»ΜΚσ±»Ϋœ¥σ–ΓΘ§≈–Εœ≥ωΥ≠ΒΡΉέΚœ≥…Φ®ΉνΗΏΘ§Φ¥Ω…≈–Εœ≥ωΥ≠ΫΪ±Μ¬Φ”Ο.
ΫβΘΚ(1)![]() =(94+89+90)Γ¬3=273Γ¬3=91(Ζ÷)Θ§
=(94+89+90)Γ¬3=273Γ¬3=91(Ζ÷)Θ§
![]() =(92+90+94)Γ¬3=276Γ¬3=92(Ζ÷)Θ§
=(92+90+94)Γ¬3=276Γ¬3=92(Ζ÷)Θ§
![]() =(91+88+94)Γ¬3=273Γ¬3=91(Ζ÷)Θ§
=(91+88+94)Γ¬3=273Γ¬3=91(Ζ÷)Θ§
ΓύΦΉΒΡΟφ ‘≥…Φ®ΒΡΤΫΨυΖ÷![]() «91Ζ÷Θ§““ΒΡΟφ ‘≥…Φ®ΒΡΤΫΨυΖ÷
«91Ζ÷Θ§““ΒΡΟφ ‘≥…Φ®ΒΡΤΫΨυΖ÷![]() «92Ζ÷Θ§±ϊΒΡΟφ ‘≥…Φ®ΒΡΤΫΨυΖ÷
«92Ζ÷Θ§±ϊΒΡΟφ ‘≥…Φ®ΒΡΤΫΨυΖ÷![]() «91Ζ÷ΘΜ
«91Ζ÷ΘΜ
(2)ΦΉΒΡΉέΚœ≥…Φ®=40%ΓΝ95+60%ΓΝ91=38+54.6=92.6(Ζ÷)Θ§
““ΒΡΉέΚœ≥…Φ®=40%ΓΝ94+60%ΓΝ92=37.6+55.2=92.8(Ζ÷)Θ§
±ϊΒΡΉέΚœ≥…Φ®=40%ΓΝ94+60%ΓΝ91=37.6+54.6=92.2(Ζ÷)Θ§
ΓΏ92.8ΘΨ92.6ΘΨ92.2Θ§
Γύ““ΫΪ±Μ¬Φ”Ο.
Ι ¥πΑΗΈΣΘΚ(1)![]() =91Ζ÷Θ§
=91Ζ÷Θ§![]() =92Ζ÷Θ§
=92Ζ÷Θ§![]() =91Ζ÷ΘΜ(2)““ΫΪ±Μ¬Φ”Ο.
=91Ζ÷ΘΜ(2)““ΫΪ±Μ¬Φ”Ο.


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
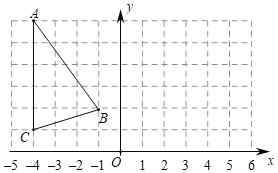
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΤΫΟφ÷±Ϋ«Ήχ±ξœΒxoy÷–A(©¹4Θ§6)Θ§B(©¹1Θ§2)Θ§C(©¹4Θ§1)Θ°
Θ®1Θ©Ής≥ωΓςABCΙΊ”Ύ÷±œΏx=1Ε‘≥ΤΒΡΆΦ–ΈΓςA1B1C1≤Δ–¥≥ωΓςA1B1C1ΗςΕΞΒψΒΡΉχ±ξΘΜ
Θ®2Θ©ΫΪΓςA1B1C1œρΉσΤΫ“Τ2ΗωΒΞΈΜΘ§Ής≥ωΤΫ“ΤΚσΒΡΓςA2B2C2Θ§≤Δ–¥≥ωΓςA2B2C2ΗςΕΞΒψΒΡΉχ±ξΘΜ
Θ®3Θ©Ιέ≤λΓςABCΚΆΓςA2B2C2Θ§ΥϋΟ« «ΖώΙΊ”ΎΡ≥÷±œΏΕ‘≥ΤΘΩ»τ «Θ§«κ÷Η≥ωΕ‘≥Τ÷αΘ§≤Δ«σΓςABCΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΒψ![]() «
«![]() ÷α’ΐΑκ÷αΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψ
÷α’ΐΑκ÷αΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψ![]() Ής
Ής![]() ÷αΒΡ¥ΙœΏ
÷αΒΡ¥ΙœΏ![]() ΫΜΥΪ«ζœΏ
ΫΜΥΪ«ζœΏ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ°
Θ°
![]() »γΆΦΦΉΘ§Β±Βψ
»γΆΦΦΉΘ§Β±Βψ![]() ‘Ύ
‘Ύ![]() ÷αΒΡ’ΐΖΫœρ…œ‘ΥΕ· ±Θ§
÷αΒΡ’ΐΖΫœρ…œ‘ΥΕ· ±Θ§![]() ΒΡΟφΜΐ¥σ–Γ «Ζώ±δΜ·ΘΩ»τ≤Μ±δΘ§«κ«σ≥ω
ΒΡΟφΜΐ¥σ–Γ «Ζώ±δΜ·ΘΩ»τ≤Μ±δΘ§«κ«σ≥ω![]() ΒΡΟφΜΐΘΜ»τΗΡ±δΘ§ ‘ΥΒΟςάμ”…ΘΜ
ΒΡΟφΜΐΘΜ»τΗΡ±δΘ§ ‘ΥΒΟςάμ”…ΘΜ
![]() »γΆΦ““Θ§‘Ύ
»γΆΦ““Θ§‘Ύ![]() ÷α…œΒΡΒψ
÷α…œΒΡΒψ![]() ΒΡ”“≤ύ”–“ΜΒψ
ΒΡ”“≤ύ”–“ΜΒψ![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() ÷αΒΡ¥ΙœΏΫΜΥΪ«ζœΏ”ΎΒψ
÷αΒΡ¥ΙœΏΫΜΥΪ«ζœΏ”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§…η
Θ§…η![]() ΒΡΟφΜΐ «
ΒΡΟφΜΐ «![]() Θ§Χί–Έ
Θ§Χί–Έ![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() Θ§–¥≥ω
Θ§–¥≥ω![]() ”κ
”κ![]() ΒΡ¥σ–ΓΙΊœΒΘ®”Ο ΓΑ
ΒΡ¥σ–ΓΙΊœΒΘ®”Ο ΓΑ![]() Γ±ΓΔΓΑ
Γ±ΓΔΓΑ![]() Γ±ΓΔΓΑ
Γ±ΓΔΓΑ![]() Γ±±μ ΨΘ©ΘΜ
Γ±±μ ΨΘ©ΘΜ
![]() »γΆΦ±ϊΘ§
»γΆΦ±ϊΘ§![]() ΒΡ―”≥ΛœΏ”κΥΪ«ζœΏ
ΒΡ―”≥ΛœΏ”κΥΪ«ζœΏ![]() ΒΡΝμ“ΜΗωΫΜΒψΈΣ
ΒΡΝμ“ΜΗωΫΜΒψΈΣ![]() Θ§
Θ§![]() ¥Ι÷±”Ύ
¥Ι÷±”Ύ![]() ÷αΘ§¥ΙΉψΈΣΒψ
÷αΘ§¥ΙΉψΈΣΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§
Θ§![]() Θ§ ‘÷ΛΟςΥΡ±Ώ–Έ
Θ§ ‘÷ΛΟςΥΡ±Ώ–Έ![]() ΒΡΟφΜΐΈΣ“ΜΗω≥Θ ΐΘ°
ΒΡΟφΜΐΈΣ“ΜΗω≥Θ ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
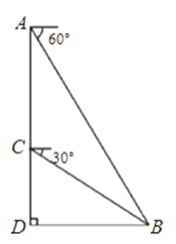
ΓΨΧβΡΩΓΩ«ύ«ύ≤ί‘≠…œΘ§Μ“ΧΪά«ΟΩΧλΕΦœκΉ≈»γΚΈΉΞ―ρΘ§Εχ«“ «¬≈Αή¬≈ ‘Θ§”ά≤Μ―‘ΤζΘ§Θ®»γΆΦΥυ ΨΘ©“ΜΧλΘ§Μ“ΧΪά«‘ΎΉ‘Φ“≥«±ΛΕΞ≤ΩA¥Π≤βΒΟάΝ―ρ―ρΥυ‘ΎΒΊB¥ΠΒΡΗ©Ϋ«ΈΣ60ΓψΘ§»ΜΚσœ¬ΒΫ≥«±ΛΒΡC¥ΠΘ§≤βΒΟB¥ΠΒΡΗ©Ϋ«ΈΣ30ΓψΘ°“―÷ΣAC=50ΟΉΘ§»τΜ“ΧΪά«“‘5m/sΒΡΥΌΕ»¥”≥«±ΛΒΉ≤ΩD¥Π≥ωΖΔΘ§άΝ―ρ―ρ“‘3m/s―ΊDB―”≥ΛœΏΖΫœρΧ”≈ήΘ§Μ“ΧΪά«ΦΗΟκ÷”ΚσΡήΉΞΒΫάΝ―ρ―ρΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
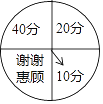
ΓΨΧβΡΩΓΩΓΑΈε“ΜΓ±ΦΌ»’ΤΎΦδΘ§Ρ≥ΆχΒξΈΣΝΥ¥ΌœζΘ§…ηΦΤΝΥ“Μ÷÷≥ιΫ±ΥΆΜΐΖ÷ΜνΕ·Θ§‘ΎΗΟΆχΒξΆχ“≥…œœ‘ Ψ»γΆΦΥυ ΨΒΡ‘≤–ΈΉΣ≈ΧΘ§ΉΣ≈Χ±ΜΨυΒ»ΒΡΖ÷≥…ΥΡΖίΘ§ΥΡΗω…»–Έ…œΖ÷±π±ξ”–ΓΑ–Μ–ΜΜίΙΥΓ±ΓΔΓΑ10Ζ÷Γ±ΓΔΓΑ20Ζ÷Γ±ΓΔΓΑ40Ζ÷Γ±Ή÷―υΘ°≤Έ”κ≥ιΫ±ΒΡΙΥΩΆ÷Μ–η”Ο σ±ξΒψΜςΉΣ≈ΧΘ§÷Η’κΨΆΜα‘ΎΉΣΕ·ΒΡΙΐ≥Χ÷–ΥφΜζΒΡΆΘ‘ΎΡ≥Ηω…»–Έ«χ”ρΘ§÷Η’κ÷Ηœρ…»–Έ…œΒΡΜΐΖ÷ΨΆ «ΙΥΩΆΜώΒΟΒΡΫ±άχΜΐΖ÷Θ§Ζ≤ «‘ΎΜνΕ·ΤΎΦδœ¬ΒΞΒΡΙΥΩΆΘ§ΨυΩ…ΜώΒΟΝΫ¥Έ≥ιΫ±ΜζΜαΘ§«σΝΫ¥Έ≥ιΫ±ΙΥΩΆΜώΒΟΒΡΉήΜΐΖ÷≤ΜΒΆ”Ύ30Ζ÷ΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣAB «Γ―OΒΡ÷±ΨΕΘ§ΒψCΓΔD‘ΎΓ―O…œΘ§ΒψE‘ΎΓ―OΆβΘ§ΓœEAC=ΓœB=60ΓψΘ°
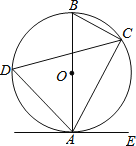
Θ®1Θ©«σΓœADCΒΡΕ» ΐΘΜ
Θ®2Θ©«σ÷ΛΘΚAE «Γ―OΒΡ«–œΏΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΒψO «AC±Ώ…œ“ΜΕ·ΒψΘ§ΙΐΒψOΉςBCΒΡΤΫ––œΏΫΜΓœACBΒΡΫ«ΤΫΖ÷œΏ”ΎΒψEΘ§ΫΜΓœACBΒΡΆβΫ«ΤΫΖ÷œΏ”ΎΒψF
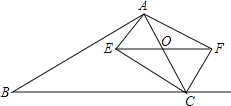
Θ®1Θ©«σ÷ΛΘΚEOΘΫFOΘΜ
Θ®2Θ©Β±ΒψO‘ΥΕ·ΒΫΚΈ¥Π ±Θ§ΥΡ±Ώ–ΈCEAF «ΨΊ–ΈΘΩ«κ÷ΛΟςΡψΒΡΫα¬έΘ°
Θ®3Θ©‘ΎΒΎΘ®2Θ©Έ ΒΡΫα¬έœ¬Θ§»τAEΘΫ3Θ§ECΘΫ4Θ§ABΘΫ12Θ§BCΘΫ13Θ§«κ÷±Ϋ”–¥≥ωΑΦΥΡ±Ώ–ΈABCEΒΡΟφΜΐΈΣΓΓ ΓΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―≈άώΦ·Ά≈Ρ≥―ß–ΘΫΧ―ß¬Ξ–η“Σ‘ΎΙφΕ® ±ΦδΡΎΫ®‘λΆξ≥…Θ§“‘±Η”≠Ϋ”–¬―ßΤΎΒΡΩΣ―ßΘ§‘ΎΙΛ≥Χ’–±ξ ±Θ§Ϋ”ΒΫΦΉΓΔ““ΝΫΗωΙΛ≥ΧΕ”ΒΡΆΕ±ξ ι»γœ¬ΘΚ(≤ΩΖ÷–≈œΔ)


―ß–ΘΚσ«Ύ¥ΠΧα≥ωΝΫΗωΖΫΑΗΘΚΔΌ”…ΦΉΙΛ≥ΧΕ”Εά ©ΙΛΘΜΔΎ”…““ΙΛ≥ΧΕ”ΒΞΕά ©ΙΛΘΜ
–ΘΆ≈Έ·―ß…ζ¥ζ±μ–ΓΉιΗυΨίΦΉΓΔ““ΝΫΕ”ΒΡΆΕ±ξ ι≤βΥψΦΑΙΛΤΎΑ≤≈≈Θ§Χα≥ωΝΥ–¬ΒΡΖΫΑΗΘΚ
Δέ»τΦΉ““ΝΫΕ”ΚœΉω4ΧλΘ§”ύœ¬ΒΡΙΛ≥Χ”…““Ε”ΒΞΕάΉω“≤’ΐΚΟ»γΤΎΆξ≥…Θ°
‘Έ ΘΚ(1)―ß–ΘΙφΕ®ΒΡΤΎœό «Εύ…ΌΧλΘΩ
(2)‘Ύ≤ΜΒΔΈσΙΛΤΎΒΡ«ΑΧαœ¬Θ§ΡψΨθΒΟΡΡ“Μ÷÷ ©ΙΛΖΫΑΗΉνΫΎ ΓΙΛ≥ΧΩνΘΩ«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
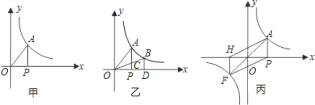
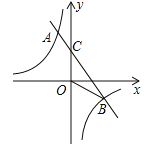
ΓΨΧβΡΩΓΩ»γΆΦΘ§“Μ¥ΈΚ· ΐy=kx+bΘ®kΓΌ0Θ©ΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐ![]() ΒΡΆΦœσœύΫΜ”ΎAΘ®-1Θ§mΘ©Θ§BΘ®nΘ§-1Θ©ΝΫΒψΘ§÷±œΏAB”κy÷αΫΜ”ΎCΒψΘ§Ν§Ϋ”OBΘ°
ΒΡΆΦœσœύΫΜ”ΎAΘ®-1Θ§mΘ©Θ§BΘ®nΘ§-1Θ©ΝΫΒψΘ§÷±œΏAB”κy÷αΫΜ”ΎCΒψΘ§Ν§Ϋ”OBΘ°
Θ®1Θ©«σ“Μ¥ΈΚ· ΐΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©‘Ύx÷α…œ’““ΜΒψPΘ§Ν§Ϋ”BPΘ§ ΙΓςBOPΒΡΟφΜΐΒ»”ΎΓςBOCΒΡΟφΜΐΒΡ2±ΕΘ§«σ¬ζΉψΧθΦΰΒΡΒψPΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com