
【题目】关于x的方程![]() ,
,
(1)a为何值时,方程的一根为0?
(2)a为何值时,两根互为相反数?
(3)试证明:无论a取何值,方程的两根不可能互为倒数.
【答案】(1)a=1时,方程的一根为0;
(2)当a=2时,原方程的两根互为相反数;
(3)无论a取何值,方程的两根不可能互为倒数.
【解析】
试题(1)若方程的一根为0,则两根的积必为0,根据此关系可求出a的值;
(2)根据相反数的概念及一元二次方程两根之和与系数的关系解答即可;
(3)根据倒数的概念及一元二次方程两根之积与系数的关系证明即可.
试题解析:(1)∵关于x的方程2x2﹣(a2﹣4)x﹣a+1=0,一根为0,
∴![]() =0,
=0,
∴﹣a+1=0,解得a=1,
∴a=1时,方程的一根为0;
(2)∵关于x的方程2x2﹣(a2﹣4)x﹣a+1=0,两根互为相反数,
∴![]() =0,解得:a=±2;
=0,解得:a=±2;
把a=2代入原方程得,2x2﹣1=0,x=±![]() ,
,
把a=﹣2代入原方程得,2x2+3=0,x2=![]() ,无解.
,无解.
故当a=2时,原方程的两根互为相反数;
(3)因为互为倒数的两个数积为1,所以x1x2=![]() =1,
=1,
即![]() =1,
=1,
解得,a=﹣1,
把a=﹣1代入原方程得,2x2+3x+2=0,
∵△=32﹣4×2×2=﹣7<0,
∴原方程无解,
∴无论a取何值,方程的两根不可能互为倒数.


科目:初中数学 来源: 题型:
【题目】[问题情境]
已知矩形的面积为一定值1,当该矩形的一组邻边分别为多少时,它的周长最小?最小值是多少?
[数学模型]
设该矩形的一边长为x,周长为L,则L与x的函数表达式为 .
[探索研究]
小彬借鉴以前研究函数的经验,先探索函数![]() 的图象性质.
的图象性质.
(1)结合问题情境,函数![]() 的自变量x的取值范围是 ,
的自变量x的取值范围是 ,
如表是y与x的几组对应值.
x | … |
|
|
| 1 | 2 | 3 | m | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
①直接写出m的值;
②画出该函数图象,结合图象,得出当x= 时,y有最小值,y的最小值为 .
[解决问题]
(2)直接写出“问题情境”中问题的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
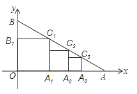
【题目】如图,在平面直角坐标系中,点A(![]() ,0),点B(0,1),作第一个正方形OA1C1B1且点A1在OA上,点B1在OB上,点C1在AB上;作第二个正方形A1A2C2B2且点A2在A1A上,点B2在A1C2上,点C2在AB上…,如此下去,则点Cn的纵坐标为________.
,0),点B(0,1),作第一个正方形OA1C1B1且点A1在OA上,点B1在OB上,点C1在AB上;作第二个正方形A1A2C2B2且点A2在A1A上,点B2在A1C2上,点C2在AB上…,如此下去,则点Cn的纵坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
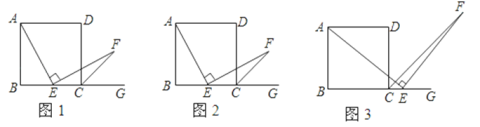
如图,在正方形ABCD中,点E是线段BG上的动点,AE⊥EF,EF交正方形外角∠DCG的平分线CF于点F.
(探究展示)
(1)如图1,若点E是BC的中点,证明:∠BAE+∠EFC=∠DCF.
(2)如图2,若点E是BC的上的任意一点(B、C除外),∠BAE+∠EFC=∠DCF是否仍然成立?若成立,请予以证明;若不成立,请说明理由.
(拓展延伸)
(3)如图3,若点E是BC延长线(C除外)上的任意一点,求证:AE=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
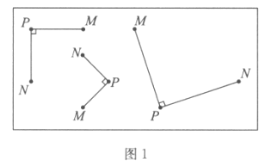
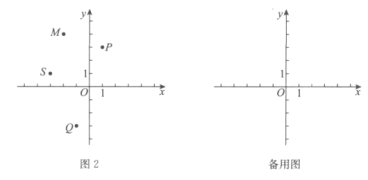
【题目】如图1中的三种情况所示,对于平面内的点M,点N,点P,如果将线段PM绕点P顺时针旋转90°能得到线段PN,就称点N是点M关于点P的“正矩点”.
(1)在如图2所示的平面直角坐标系![]() 中,已知
中,已知![]() ,
,![]() .
.
①在点P,点Q中,___________是点S关于原点O的“正矩点”;
②在S,P,Q,M这四点中选择合适的三点,使得这三点满足:
点_________是点___________关于点___________的“正矩点”,写出一种情况即可;
(2)在平面直角坐标系![]() 中,直线
中,直线![]() 与x轴交于点A,与y轴交于点B,点A关于点B的“正矩点”记为点C,坐标为
与x轴交于点A,与y轴交于点B,点A关于点B的“正矩点”记为点C,坐标为![]() .
.
①当点A在x轴的正半轴上且OA小于3时,求点C的横坐标![]() 的值;
的值;
②若点C的纵坐标![]() 满足
满足![]() ,直接写出相应的k的取值范围.
,直接写出相应的k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(5,0),B(0,5).
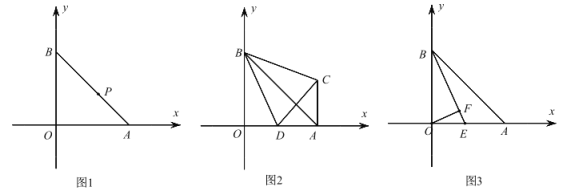
(1)如图 1,P 是 AB 上一点且![]()
![]() ,求 P 点坐标;
,求 P 点坐标;
(2)如图 2,D 为 OA 上一点,AC∥OB 且∠CBO=∠DCB,求∠CBD 的度数;
(3)如图 3,E 为 OA 上一点,OF⊥BE 于 F,若∠BEO=45°+∠EOF,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=![]() 的图象如图所示,则以下结论:①m<0;②在每个分支上y随x的增大而增大;③若点A(-1,a),点B(2,b)在图象上,则a <b;④若点P(x,y)在图象上,则点P1(-x,y)也在图象上.其中正确的个数为( )
的图象如图所示,则以下结论:①m<0;②在每个分支上y随x的增大而增大;③若点A(-1,a),点B(2,b)在图象上,则a <b;④若点P(x,y)在图象上,则点P1(-x,y)也在图象上.其中正确的个数为( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
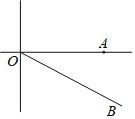
【题目】如图,A城气象台测得台风中心在A城正西方向240km的O处,以每小时40km的速度向南偏东60°的OB方向移动,距台风中心130km的范围内是受台风影响的区域.
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到台风的影响,求出受台风影响的时间有多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com