
【题目】在平面直角坐标系中,A(5,0),B(0,5).
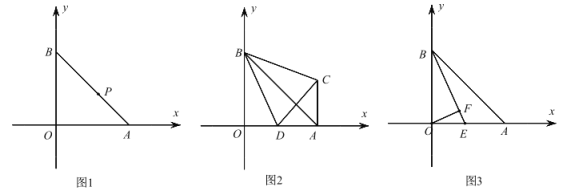
(1)如图 1,P 是 AB 上一点且![]()
![]() ,求 P 点坐标;
,求 P 点坐标;
(2)如图 2,D 为 OA 上一点,AC∥OB 且∠CBO=∠DCB,求∠CBD 的度数;
(3)如图 3,E 为 OA 上一点,OF⊥BE 于 F,若∠BEO=45°+∠EOF,求![]() 的值
的值
【答案】(1)(3,2) (2)45° (3)2
【解析】
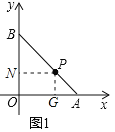
(1)作PG⊥x轴于G,PN⊥y轴于N,根据相似三角形的性质列出比例式,分别求出PG,PN,得到P点坐标;
(2)作BG⊥AC交AC的延长线于G,作BH⊥CD于H,分别证明△BCH≌△BCG和Rt△BOD≌Rt△BHD,根据全等三角形的性质得到∠CBH=∠CBG,∠BOD=∠HOD,结合图形计算;
(3)根据题意和三角形内角和定理分别求出∠BEO=67.5°,∠EOF=22.5°,作∠BOP=∠OBE,设OF=a,根据三角形外角的性质,相似三角形的性质分别求出BF,EF,代入计算即可.
(1)作PG⊥x轴于G,PN⊥y轴于N,
∵![]()
![]()
∴![]()
∵A(5,0),B(0,5),
∴OA=5,OB=5,
∵PG⊥x轴,
∴PG∥OB,
∴△AGP∽△AOB,
∴![]() ,即
,即![]() ,
,
解得,PG=2,
同理,PN=3,
∴P点坐标为(3,2);
(2)作BG⊥AC交AC的延长线于G,作BH⊥CD于H,
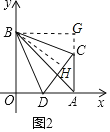
∴四边形BOAG为矩形,
∴BO=BG,
∵OA=OB,
∴矩形BOAG为正方形,
∵AC∥OB
∴∠CBO=∠BCG,
∵∠CBO=∠DCB,
∴∠BCG=∠DCB,
在△BCH和△BCG中,
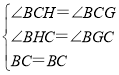 ,
,
∴△BCH≌△BCG(AAS),
∴∠CBH=∠CBG,BG=BH,
∴BO=BH,
在Rt△BOD和Rt△BHD中,
![]()
∴Rt△BOD≌Rt△BHD(HL),
∴∠BOD=∠HOD,
∴∠CBD=∠DBH+∠CBH=![]() ∠OBG=45°;
∠OBG=45°;
(3)
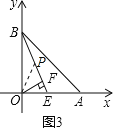
∵∠BEO=45°+∠EOF,∠BEO+∠EOF=90°,
∴∠BEO=67.5°,∠EOF=22.5°,
则∠OBE=22.5°,
作∠BOP=∠OBE=22.5°,
则PB=PO,∠OPF=45°,
设OF=a,则PF=OF=a,
由勾股定理得,OP=![]() a,
a,
∴PB=![]() a,
a,
∴BF=![]() a+a,
a+a,
∵∠BOP=∠OBE,∠OFB=∠EFO=90°,
∴△OFB∽△EFO,
∴EF=![]() a-a,
a-a,
∴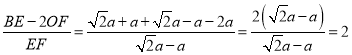


科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=30°,∠ACB=45°,BD∥AC,BD=AB,且C,D两点位于AB所在直线两侧,射线AD上的点E满足∠ABE=60°.
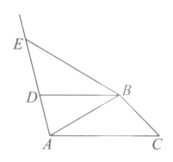
(1)∠AEB=___________°;
(2)图中与AC相等的线段是_____________,证明此结论只需证明△________≌△_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,(图1,图2),四边形ABCD是边长为4的正方形,点E在线段BC上,∠AEF=90°,且EF交正方形外角平分线CP于点F,交BC的延长线于点N, FN⊥BC.
(1)若点E是BC的中点(如图1),AE与EF相等吗?
(2)点E在BC间运动时(如图2),设BE=x,△ECF的面积为y。
①求y与x的函数关系式;
②当x取何值时,y有最大值,并求出这个最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
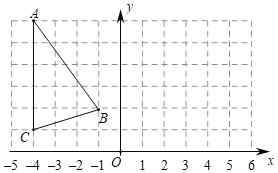
【题目】如图,平面直角坐标系xoy中A(﹣4,6),B(﹣1,2),C(﹣4,1).
(1)作出△ABC关于直线x=1对称的图形△A1B1C1并写出△A1B1C1各顶点的坐标;
(2)将△A1B1C1向左平移2个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△ABC和△A2B2C2,它们是否关于某直线对称?若是,请指出对称轴,并求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一只电子狗从原点O出发,按向上→向右→向下→向下→向右的方向依次不断移动,每次移动1个单位长度,其行走路线如图所示,则A2018的坐标为( )
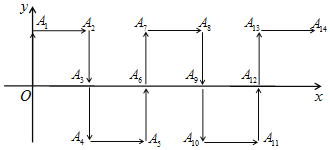
A.(337,1)B.(337,﹣1)C.(673,1)D.(673,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A 1.5小时以上;B 1~1.5小时;C 0.5~1小时;D 0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:

(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
查看答案和解析>>
科目:初中数学 来源: 题型:
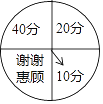
【题目】“五一”假日期间,某网店为了促销,设计了一种抽奖送积分活动,在该网店网页上显示如图所示的圆形转盘,转盘被均等的分成四份,四个扇形上分别标有“谢谢惠顾”、“10分”、“20分”、“40分”字样.参与抽奖的顾客只需用鼠标点击转盘,指针就会在转动的过程中随机的停在某个扇形区域,指针指向扇形上的积分就是顾客获得的奖励积分,凡是在活动期间下单的顾客,均可获得两次抽奖机会,求两次抽奖顾客获得的总积分不低于30分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com