
【题目】现场学习题:
问题背景:
在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积.
,求这个三角形的面积.
小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.
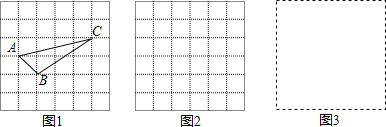
(1)请你将△ABC的面积直接填写在横线上. .
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法,若△ABC三边的长分别为![]() a,2
a,2![]() a、
a、![]() a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是: .
a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是: .
探索创新:
(3)若△ABC三边的长分别为![]() 、
、![]() 、
、![]() (m>0,n>0,m≠n),请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为: .
(m>0,n>0,m≠n),请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为: .
【答案】(1)2.5;(2)画图详见解析;3a2;(3)画图详见解析;3mn.
【解析】
(1)把△ABC所在长方形画出来,再用矩形的面积减去周围多余三角形的面积即可;
(2)![]() a是直角边长为a、a的直角三角形的斜边;2
a是直角边长为a、a的直角三角形的斜边;2![]() a是直角边长为4a,2a的直角三角形的斜边;
a是直角边长为4a,2a的直角三角形的斜边;![]() a是直角边长为a,5a的直角三角形的斜边,把它整理为一个矩形的面积减去三个直角三角形的面积;
a是直角边长为a,5a的直角三角形的斜边,把它整理为一个矩形的面积减去三个直角三角形的面积;
(3)结合(1),(2)易得此三角形的三边分别是直角边长为n,4m的直角三角形的斜边;直角边长为2m,2n的直角三角形的斜边;直角边长为2m,n的直角三角形的斜边.同样把它整理为一个矩形的面积减去三个直角三角形的面积.
(1)S△ABC=4×2-![]() ×4×1-
×4×1-![]() ×1×1-
×1×1-![]() ×2×3=2.5,
×2×3=2.5,
故答案为:2.5;
(2)如图所示:
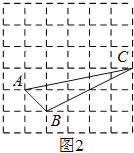
S△ABC=5a×2a-![]() ×a×a-
×a×a-![]() ×2a×4a-
×2a×4a-![]() ×a×5a=3a2,
×a×5a=3a2,
故答案为:3a2;
(3)如图所示:
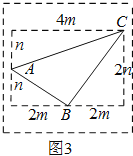
S△ABC=4m×2n-![]() ×2m×2n-
×2m×2n-![]() ×2m×n-
×2m×n-![]() ×4m×n=3mn,
×4m×n=3mn,
故答案为:3mn.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】已知一抛物线与x轴的交点是A(﹣2,0),B(1,0),且经过点C(2,8).
(1)求该抛物线的解析式,并写出顶点坐标.
(2)直接写出当y>8时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两台机床同时加工直径为![]() 的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取
的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取![]() 件进行检测,结果如下(单位:
件进行检测,结果如下(单位:![]() ):
):
甲 |
|
|
|
|
|
乙 |
|
|
|
|
|
(1)分别求出这两台机床所加工零件直径的平均数和方差;
(2)根据所学的统计知识,你认为哪一台机床生产零件的稳定性更好一些,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,晚上小亮在广场上乘凉,图中线段AB表示站在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯.
请你再图中画出小亮在照明灯P照射下的影子BC;
如果灯杆高PO=12m,小亮的身高AB=1.6m,小亮与灯杆的距离BO=13m,请求出小亮影子的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂拟建一座平面图形为矩形且面积为200平方米的三级污水处理池(平面图如图ABCD所示).由于地形限制,三级污水处理池的长、宽都不能超过16米.如果池的外围墙建造单价为每米400元,中间两条隔墙建造单价为每米300元,池底建造单价为每平方米80元.(池墙的厚度忽略不计)当三级污水处理池的总造价为47200元时,求池长x.
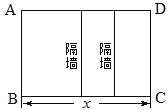
查看答案和解析>>
科目:初中数学 来源: 题型:
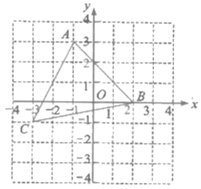
【题目】如图,在平面直角坐标系中有一个![]() ,顶点
,顶点![]() ,
,![]() ,
,![]() .
.
(1)画出![]() 关于y轴的对称图形
关于y轴的对称图形![]() (不写画法);
(不写画法);
(2)点![]() 关于
关于![]() 轴对称的点的坐标为__________,点
轴对称的点的坐标为__________,点![]() 关于
关于![]() 轴对称的点的坐标为__________;
轴对称的点的坐标为__________;
(3)若网格上每个小正方形的边长为1,求![]() 的面积?
的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地教育局为了解该地八年级学生参加社会实践活动情况,随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图:
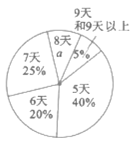

请根据图中提供的信息,回答下列问题:
(1)![]() ___________,并写出该扇形所对圆心角的度数为___________,请补全条形统计图.
___________,并写出该扇形所对圆心角的度数为___________,请补全条形统计图.
(2)在这次抽样调查中,众数为___________,中位数为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,点
中,点![]() 是线段
是线段![]() 上一动点,
上一动点, ![]() 为
为![]() 的中点,
的中点, ![]() 的延长线交BC于
的延长线交BC于![]() .
.

(1)求证: ![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 从点
从点![]() 出发,以l
出发,以l![]() 的速度向
的速度向![]() 运动(不与
运动(不与![]() 重合).设点
重合).设点![]() 运动时间为
运动时间为![]() ,请用
,请用![]() 表示
表示![]() 的长;并求
的长;并求![]() 为何值时,四边形
为何值时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com