
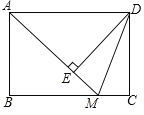
【题目】如图,在矩形ABCD中,M为BC上的点,过点D作DE⊥AM于E,DE=DC=5,AE=2EM.
(1)求证:BM=AE;
(2)求BM的长.
科目:初中数学 来源: 题型:
【题目】现场学习题:
问题背景:
在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积.
,求这个三角形的面积.
小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.
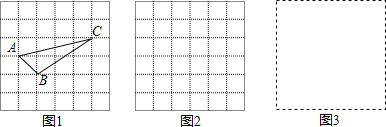
(1)请你将△ABC的面积直接填写在横线上. .
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法,若△ABC三边的长分别为![]() a,2
a,2![]() a、
a、![]() a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是: .
a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是: .
探索创新:
(3)若△ABC三边的长分别为![]() 、
、![]() 、
、![]() (m>0,n>0,m≠n),请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为: .
(m>0,n>0,m≠n),请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有完全相同的三个小球,球上分别标上数字-1、1、2.随机摸出一个小球(不放回),其数字记为p,再随机摸出另一个小球,其数字记为q,则p,q使关于x的方程x2+px+q=0有实数根的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车产业的发展,有效促进我国现代化建设.某汽车销售公司2016年盈利1500万元,到2018年盈利2160万元,且从2016年到2018年,每年盈利的年增长率相同.
(1)求每年盈利的年增长率;
(2)若该公司盈利的年增长率继续保持不变,那么2019年该公司盈利能否达到2500万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
问题发现:学完四边形的有关知识后,创新小组的同学进一步研究特殊的四边形,发现了一个结论.如图1,已知四边形![]() 是正方形,根据勾股定理和正方形的性质,很容易能够证明
是正方形,根据勾股定理和正方形的性质,很容易能够证明![]() .
.
问题探究:
(1)如图2,已知四边形![]() 是矩形,若
是矩形,若![]() ,则
,则![]() 的值是 ;
的值是 ;![]() 的值是 ;
的值是 ;
(2)如图3,已知四边形![]() 是菱形,证明:
是菱形,证明:![]() ;
;
拓广探索:
(3)智慧小组看了创新小组交流后,提出了一个猜想,如图4,在![]() 中,
中,![]() ,你认为这个猜想正确吗?请说明理由;
,你认为这个猜想正确吗?请说明理由;
(4)请用文字语言叙述![]() 中得出的结论.
中得出的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
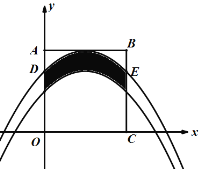
【题目】如图,抛物线y=-![]() x2+x+c的顶点是正方形ABCO的边AB的中点,点A,C在坐标轴上,抛物线分别与AO,BC交于D,E两点,将抛物线向下平移1个单位长度得到如图所示的阴影部分.现随机向该正方形区域投掷一枚小针,则针尖落在阴影部分的概率P=_________.
x2+x+c的顶点是正方形ABCO的边AB的中点,点A,C在坐标轴上,抛物线分别与AO,BC交于D,E两点,将抛物线向下平移1个单位长度得到如图所示的阴影部分.现随机向该正方形区域投掷一枚小针,则针尖落在阴影部分的概率P=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,则以下结论:①
,则以下结论:①![]() 是等腰三角形;②
是等腰三角形;②![]() 是
是![]() 的角平分线;③
的角平分线;③![]() 的周长
的周长![]() ;④
;④![]() 正确的有( )
正确的有( )
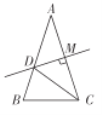
A.①②B.①③C.③④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别在AB,BC上,且AE=BF.
(1)试探索线段AF,DE的数量关系,写出你的结论并说明理由;
(2)连接EF,DF,分别取AE,EF,FD,DA的中点H,I,J,K,则四边形HIJK是什么特殊四边形?请在图2中补全图形,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com