
����Ŀ���ۺ���ʵ����
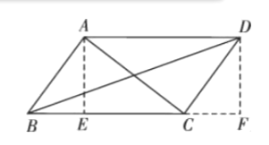
���ⷢ�֣�ѧ���ı��ε��й�֪ʶ����С���ͬѧ��һ���о�������ı��Σ�������һ�����ۣ���ͼ1����֪�ı���![]() �������Σ����ݹ��ɶ����������ε����ʣ��������ܹ�֤��
�������Σ����ݹ��ɶ����������ε����ʣ��������ܹ�֤��![]() ��
��
����̽����
��1����ͼ2����֪�ı���![]() �Ǿ��Σ���
�Ǿ��Σ���![]() ����
����![]() ��ֵ�� ��
��ֵ�� ��![]() ��ֵ�� ��
��ֵ�� ��
��2����ͼ3����֪�ı���![]() �����Σ�֤����
�����Σ�֤����![]() ��
��
�ع�̽����
��3���ǻ�С�鿴�˴���С�齻���������һ�����룬��ͼ4����![]() �У�
�У�![]() ������Ϊ���������ȷ����˵�����ɣ�
������Ϊ���������ȷ����˵�����ɣ�
��4������������������![]() �еó��Ľ��ۣ�
�еó��Ľ��ۣ�

���𰸡���1��50��50����2������������3����ȷ�����ɼ���������4���𰸲�Ψһ�����磺��ƽ���ı������Խ��ߵ�ƽ���͵��������ߵ�ƽ����������ƽ���ı��ε������ߵ�ƽ���͵������Խ��ߵ�ƽ������
��������
��1�����ݾ��ε����ʿɵã�AB��CD��4��BC��AD��3�����ݹ��ɶ����ɵ�![]() ��
��![]() ���̶���⣻
���̶���⣻
��2���������ε����ʿɵã�AC��BD��AB��BC��CD��AD��OA��OC��OB��OD�����ݹ��ɶ���������֤��
��3������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��
��![]() �ӳ����ڵ�
�ӳ����ڵ�![]() �����ı���
�����ı���![]() ��ƽ���ı��Σ���֤Rt��ABE��Rt��DCF���ó�BE��CF���ɹ��ɶ����������
��ƽ���ı��Σ���֤Rt��ABE��Rt��DCF���ó�BE��CF���ɹ��ɶ����������
![]() ��
�� ![]() ���̶���֤��
���̶���֤��
��4�������⣨3����֤������ɽ��
�⣺��1�� �ھ���ABCD�У�AB��4��BC��3����ABC����BCD����ADC����BAD��90��
��AB��CD��4��BC��AD��3��
��Rt��ABC�У��ɹ��ɶ����ɵã�
![]()
��Rt��BCD�У��ɹ��ɶ����ɵã�
![]()
��![]()
��BC��AD��3��
��![]()
��![]()
![]() ֤����
֤����![]() �ı���
�ı���![]() ������
������
![]() ��AB��BC��CD��AD��OA��OC��OB��OD��
��AB��BC��CD��AD��OA��OC��OB��OD��
��![]() �У��ɹ��ɶ�������
�У��ɹ��ɶ�������![]()
ͬ�����ɵ�![]()
![]()
![]()
![]()
![]()
![]()
![]() ���������ȷ
���������ȷ
�������£�
��ͼ������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��
��![]() �ӳ����ڵ�
�ӳ����ڵ�![]() .
.
![]() �ı���
�ı���![]() ��ƽ���ı���
��ƽ���ı���
![]()
![]()
![]()
![]()
���ݹ��ɶ�������
![]()
![]()
![]()
![]()
![]()
![]()
![]() �𰸲�Ψһ�����磺��ƽ���ı������Խ��ߵ�ƽ���͵��������ߵ�ƽ����������ƽ���ı��ε������ߵ�ƽ���͵������Խ��ߵ�ƽ��������
�𰸲�Ψһ�����磺��ƽ���ı������Խ��ߵ�ƽ���͵��������ߵ�ƽ����������ƽ���ı��ε������ߵ�ƽ���͵������Խ��ߵ�ƽ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
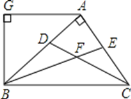
����Ŀ����ͼ��AB��AC��CD��BE�ֱ�����ABC�Ľ�ƽ���ߣ�AG��BC��AG��BG�����н��ۣ��١�BAG=2��ABF����BAƽ�֡�CBG���ۡ�ABG=��ACB���ܡ�CFB=135����������ȷ�Ľ����ǣ�������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ����1��0������3��0������ͬʱ����A��B���ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��CD����ƽ���ı���ABDC��
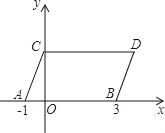
��1��ֱ��д����C��D�����ꣻ
��2������ֱ��CD�ϴ��ڵ�M������MA��MB��ʹS��MAB��2S��MBD�������M�����ꣻ
��3������P��ֱ��BD���˶�������PC��PO���뻭��ͼ�Σ�д����CPO����DCP����BOP��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ����������������ȷ���ǣ� ��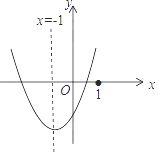
A.a��b��c
B.һ�κ���y=ax+c��ͼ����������
C.m��am+b��+b��a��m������ʵ����
D.3b+2c��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��Ϊ���꼶ͬѧ��ף���һ������ͯ�ڡ���������Ҫ�����ʻ�266�䣬�����ʻ�169�䣬�Ƴ�A��B��������16����Ҫ��A�����ü����ʻ�18�䣬�����ʻ�10�䣻B�����ü����ʻ�16�䣬�����ʻ�11�䣬��ij����������
��1�����깲�м��������������ֱ����ļ��֣�
��2����A������ÿ���ʻ��ɻ������12Ԫ��B������ÿ���ʻ��ɻ������10Ԫ��������ǵ�������ѡ����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ABC��λ����ͼ��ʾ��ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ���
�ٽ���ABC��x�᷽������ƽ��6����λ���ȣ�����ƽ�ƺ�õ��ġ�A1B1C1��
�ڽ���ABC���ŵ�A˳ʱ����ת90�㣬������ת��õ��ġ�AB2C2��
��ֱ��д����B2 �� C2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ij�羰����������Ϣ��
�������� | �շѱ� |
������30�� | �˾��շ�80Ԫ |
����30�� | ÿ����1�ˣ��˾��շѽ���1Ԫ�����˾��շѲ�����55Ԫ |
A��˾��֯һ��Ա�����÷羰�����Σ�֧����������2800Ԫ��A��˾�μ�������ε�Ա���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ������Ϊ�߷ֱ�������������������
������Ϊ�߷ֱ�������������������![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ����
����![]() �������
�������![]() �������߶�
�������߶�![]() ��
��![]() ��
��![]() Ϊ�ߵ������ε������__________��
Ϊ�ߵ������ε������__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��y�ᣬ����ΪB������ABO�Ƶ�A��ʱ����ת����AB1O1��λ�ã�ʹ��B�Ķ�Ӧ��B1����ֱ��y=�� ![]() x�ϣ��ٽ���AB1O1�Ƶ�B1��ʱ����ת����A1B1O1��λ�ã�ʹ��O1�Ķ�Ӧ��O2����ֱ��y=��
x�ϣ��ٽ���AB1O1�Ƶ�B1��ʱ����ת����A1B1O1��λ�ã�ʹ��O1�Ķ�Ӧ��O2����ֱ��y=�� ![]() x�ϣ����ν�����ȥ������B�������ǣ�0��1�������O12��������Ϊ ��
x�ϣ����ν�����ȥ������B�������ǣ�0��1�������O12��������Ϊ �� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com