【题目】根据绍兴市某风景区的旅游信息：
旅游人数 | 收费标准 |
不超过30人 | 人均收费80元 |
超过30人 | 每增加1人，人均收费降低1元，但人均收费不低于55元 |
A公司组织一批员工到该风景区旅游，支付给旅行社2800元．A公司参加这次旅游的员工有多少人？
100分闯关期末冲刺系列答案科目：初中数学 来源： 题型：
【题目】某企业用规格是170×40的标准板材作为原材料，按照如图1所示的裁法一或裁法二，裁剪出甲型与乙型两种板材（单位：cm）
（1）求图中a，b的值；
（2）若将50张标准板材按裁法一裁剪，10张标准板材按裁法二裁剪，裁剪后将得到的甲型与乙型板材做侧面或底面，做成如图2的竖式与横式两种无盖的装饰盒若干（接缝处的长度忽略不计）．
①一共可裁剪出甲型板材______张，乙型板材______张；
②设可以做出竖式和横式两种无盖装饰盒一共x个，则x的最大值是______．
查看答案和解析>>
科目：初中数学 来源： 题型：
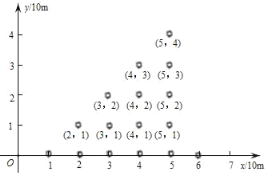
【题目】某景区有一片树林，不仅树种相同，而且排列有序，如果用平面直角坐标系来表示每一棵的具体位置，从第一棵树开始依次表示为（1，0）→（2，0）→（2，1）→（3，2）→（3，1）→（3，0）→（4.0）→……，则第100棵树的位置是____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】综合与实践：
问题发现：学完四边形的有关知识后，创新小组的同学进一步研究特殊的四边形，发现了一个结论．如图1，已知四边形
是正方形，根据勾股定理和正方形的性质，很容易能够证明
．
问题探究：
（1）如图2，已知四边形是矩形，若
，则
的值是 ；
的值是 ；
（2）如图3，已知四边形是菱形，证明：
；
拓广探索：
（3）智慧小组看了创新小组交流后，提出了一个猜想，如图4，在
中，，你认为这个猜想正确吗？请说明理由；
（4）请用文字语言叙述
中得出的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知边长为m的正方形面积为12，则下列关于m的说法中：①m2是有理数；②m的值满足m2﹣12＝0；③m满足不等式组
；④m是12的算术平方根. 正确有几个（ ）
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知△ABC在平面直角坐标系中的位置如图所示．将△ABC向右平移6个单位长度，再向下平移6个单位长度得到△A1B1C1．(图中每个小方格边长均为1个单位长度) ．
（1）在图中画出平移后的△A1B1C1；
（2）直接写出△A1B1C1各顶点的坐标．
； 
； 
；
（3）求出△ABC的面积
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】完成下面的证明过程．
如图，已知，∠1+∠2＝180°，∠A＝∠D．求证AB∥CD．
证明：∵∠1+∠2＝180°（已知）
∠1＝∠3（ ）
∴∠3+∠2＝180°（ ）
∴AE∥ （ ）
∴∠D＝ （ ）
∵∠A＝∠D（已知）
∴∠A＝∠CEA（ ）
∴AB∥CD （ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，∠A=∠C=90°，∠B=α，在AB、BC上分别找一点E、F，使△DEF的周长最小．此时，∠EDF=( )
A.αB.
C.
D.180°-2α
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
