
【题目】完成下面的证明过程.
如图,已知,∠1+∠2=180°,∠A=∠D.求证AB∥CD.
证明:∵∠1+∠2=180°(已知)
∠1=∠3( )
∴∠3+∠2=180°( )
∴AE∥ ( )
∴∠D= ( )
∵∠A=∠D(已知)
∴∠A=∠CEA( )
∴AB∥CD ( )

【答案】对顶角相等,等量代换;DF;同旁内角互补,两直线平行,∠AEC;两直线平行,同位角相等,等量代换;内错角相等,两直线平行
【解析】
求出∠2+∠3=180°,根据平行线的判定得出AE∥DF,根据平行线的性质得出∠AEC=∠D,求出∠AEC=∠A,根据平行线的判定得出即可.
证明:∵∠1+∠2=180°(已知),
又∵∠1=∠3(对顶角相等),
∴∠2+∠3=180°(等量代换),
∴AE∥DF(同旁内角互补,两直线平行),
∴∠AEC=∠D(两直线平行,同位角相等),
∵∠A=∠D(已知)
∴∠AEC=∠A(等量代换)
∴AB∥CD(内错角相等,两直线平行),
故答案为:对顶角相等,等量代换;DF;同旁内角互补,两直线平行,∠AEC;两直线平行,同位角相等,等量代换;内错角相等,两直线平行.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B,分别向上平移2个单位,再向右平移1个单位,分别得到点A、B的对应点C、D,连接AC,BD,CD,得平行四边形ABDC.
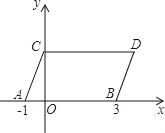
(1)直接写出点C,D的坐标;
(2)若在直线CD上存在点M,连接MA,MB,使S△MAB=2S△MBD,求出点M的坐标;
(3)若点P在直线BD上运动,连接PC,PO,请画出图形,写出∠CPO,∠DCP,∠BOP的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据绍兴市某风景区的旅游信息:
旅游人数 | 收费标准 |
不超过30人 | 人均收费80元 |
超过30人 | 每增加1人,人均收费降低1元,但人均收费不低于55元 |
A公司组织一批员工到该风景区旅游,支付给旅行社2800元.A公司参加这次旅游的员工有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来随着全国楼市的降温,商品房的价格开始呈现下降趋势,2012年某楼盘平均售价为5000元/平方米,2014年该楼盘平均售价为4050元/平方米.
(1)如果该楼盘2013年和2014年楼价平均下降率相同,求该楼价的平均下降率;
(2)按照(1)中楼价的下降速度,请你预测该楼盘2015年楼价平均是多少元/平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经营一种成本为每千克40美元的水产品,根据市场分析,若按每千克50元销售,一个月能售出500千克;销售价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况,销售单价定为多少元时,获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学准备购进A、B两种教学用具共40件,A种每件价格比B种每件价格贵8元,同时购进2件A种教学用具和3件B种教学用具恰好用去116元.
(1)求A、B两种教学用具的单价各是多少元?
(2)学校准备用不少于880元且不多于900元的金额购买A、B两种教学用具,问A种教学用具最多能购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥y轴,垂足为B,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=﹣ ![]() x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O1的位置,使点O1的对应点O2落在直线y=﹣
x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O1的位置,使点O1的对应点O2落在直线y=﹣ ![]() x上,依次进行下去…若点B的坐标是(0,1),则点O12的纵坐标为 .
x上,依次进行下去…若点B的坐标是(0,1),则点O12的纵坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的![]() 个小球,其中红球
个小球,其中红球![]() 个,白球
个,白球![]() 个.
个.
(1)先从袋子中取出![]() 个红球(
个红球(![]() 且
且![]() 为正整数),再从袋子中随机摸
为正整数),再从袋子中随机摸![]() 个小球,将“摸出白球”记为事件A,请完成下面表格:
个小球,将“摸出白球”记为事件A,请完成下面表格:
事件 | 必然事件 | 随机事件 |
|
(2)先从袋子中取出![]() 个红球,再放入
个红球,再放入![]() 个一样的白球并掘匀,随机摸出
个一样的白球并掘匀,随机摸出![]() 个白球的频率在
个白球的频率在![]() 附近摆动,求
附近摆动,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com