
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,则以下结论:①
,则以下结论:①![]() 是等腰三角形;②
是等腰三角形;②![]() 是
是![]() 的角平分线;③
的角平分线;③![]() 的周长
的周长![]() ;④
;④![]() 正确的有( )
正确的有( )
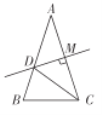
A.①②B.①③C.③④D.②④
【答案】B
【解析】
由AB=AC,∠A=36°,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,可得AD=CD,∠ABC=∠ACB=
,可得AD=CD,∠ABC=∠ACB=![]() =72°,继而求得∠ACD=∠DCB=∠A=36°,∠BDC=∠B=72°,∠CDM=54°,即可得△BCD是等腰三角形,△BCD的周长C△BCD=AB+BC,线段CD不是△BDM的角平分线,
=72°,继而求得∠ACD=∠DCB=∠A=36°,∠BDC=∠B=72°,∠CDM=54°,即可得△BCD是等腰三角形,△BCD的周长C△BCD=AB+BC,线段CD不是△BDM的角平分线,![]() 并不全等.
并不全等.
解:∵AB=AC,∠A=36°,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,
∴∠ABC=∠ACB=![]() =72°,AD=CD
=72°,AD=CD
∴∠ACD=∠DCB=∠A=36°,
∠BDC=180°-36°-72°=72°=∠B,
∠CDM=90°-36°=54°,
∴BC=DC,
故①![]() 是等腰三角形,正确;
是等腰三角形,正确;
②![]() 是
是![]() 的角平分线;错误;
的角平分线;错误;
③![]() 的周长
的周长![]() ;正确
;正确
④![]() 是直角三角形,
是直角三角形,![]() 是顶角为36°的等腰三角形,所以
是顶角为36°的等腰三角形,所以![]() 不全等,错误.
不全等,错误.
故选:B


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,点
中,点![]() 是线段
是线段![]() 上一动点,
上一动点, ![]() 为
为![]() 的中点,
的中点, ![]() 的延长线交BC于
的延长线交BC于![]() .
.

(1)求证: ![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 从点
从点![]() 出发,以l
出发,以l![]() 的速度向
的速度向![]() 运动(不与
运动(不与![]() 重合).设点
重合).设点![]() 运动时间为
运动时间为![]() ,请用
,请用![]() 表示
表示![]() 的长;并求
的长;并求![]() 为何值时,四边形
为何值时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小颖上来采取以下规定决定谁将获得仅有一张科普报告入场券:在不透明的布袋里装有除颜色之外均相同的2个红球和1个绿球,小明先取出一个球,记住颜色后放回,然后小颖再取出一个球.若两次取出的球都是红色,则小明获得入场券,否则小颖获得入场券.你认为这个规则对双方公平吗?请用画树状图或列表的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工地上有甲、乙二块铁板,铁板甲形状为等腰三角形,其顶角为![]() ,腰长为
,腰长为![]() ;铁板乙形状为直角梯形,两底边长分别为
;铁板乙形状为直角梯形,两底边长分别为![]() 、
、![]() ,且有一内角为
,且有一内角为![]() .现在我们把它们任意翻转,分别试图从一个直径为
.现在我们把它们任意翻转,分别试图从一个直径为![]() 的圆洞中穿过,结果是( )
的圆洞中穿过,结果是( )
A. 甲板能穿过,乙板不能穿过 B. 甲板不能穿过,乙板能穿过
C. 甲、乙两板都能穿过 D. 甲、乙两板都不能穿过
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地保护美丽如画的邛海湿地,西昌市污水处理厂决定先购买A,B两种型号的污水处理设备共20台,对邛海湿地周边污水进行处理.每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640 t,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1 080 t.
(1)求A,B两种型号的污水处理设备每周每台分别可以处理污水多少吨.
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4 500 t,请你列举出所有购买方案,并指出哪种方案所需资金最少,最少是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识储备
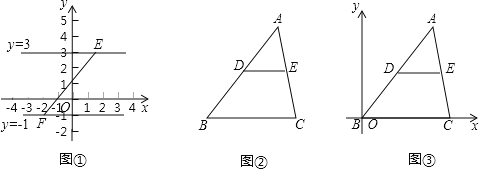
如图①,点E、F分别是y=3和y=﹣1上的动点,则EF的最小值是 ;
方法储备
直角坐标系的建立,在代数和几何之间架起了一座桥梁,用代数的方法解决几何问题:某数学小组在自主学习时了解了三角形的中位线及相关的定理,在学习了《坐标与位置)后,该小组同学深入思考,利用中点坐标公式,给出了三角形中位线定理的一种证明方法.如图②,在△ABC中,点D,E分别是AB,AC边的中点,DE称为△ABC的中位线,则DE∥BC且DE=![]() BC.该数学小组建立如图③的直角坐标系,设点A(a,b),点C (0,c)(c>0).请你利用该数学学习小组的思路证明DE∥BC且DE=
BC.该数学小组建立如图③的直角坐标系,设点A(a,b),点C (0,c)(c>0).请你利用该数学学习小组的思路证明DE∥BC且DE=![]() BC.(提示:中点坐标公式,A(x1,y1),B(x2,y2),则A,B中点坐标为(
BC.(提示:中点坐标公式,A(x1,y1),B(x2,y2),则A,B中点坐标为(![]() ,
,![]() ).
).
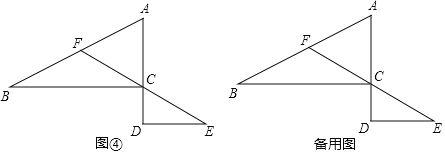
综合应用
结合上述知识和方法解决问题,如图④,在△ABC中,∠ACB=90°,AC=3,BC=6,延长AC至点 D.DE⊥AD,连接EC并延长交AB边于点F.若2CD+DE=6,则EF是否存在最小值,若存在,求出最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平行四边形![]() 在平面直角坐标系中,其中点
在平面直角坐标系中,其中点![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,点
,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,
(1)点![]() 的坐标为______,点
的坐标为______,点![]() 的坐标为_______.
的坐标为_______.
(2)求点![]() 的坐标.
的坐标.
(3)如图2,根据(2)中结论,将![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,求
,求![]() 的长度.
的长度.
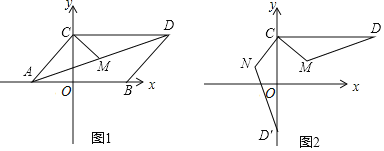
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com