【题目】如图，是抛物线形拱桥，当拱顶离水面2米时，水面宽4米．若水面下降1米，则水面宽度将增加多少米？
【答案】（2
﹣4）米
【解析】试题分析：建立平面直角坐标系，设横轴x通过AB，纵轴y通过AB中点O且通过C点，抛物线以y轴为对称轴，由题意得OC=2即抛物线顶点C坐标为（0，2），所以将抛物线解析式设为顶点式y=ax2+2，其中a可通过代入A点坐标（－2，0）到抛物线解析式得出，当水面下降1米，通过抛物线在图上的观察可转化为：当y=－1时，对应的抛物线上两点之间的距离，也就是直线y=－1与抛物线相交的两点之间的距离，将y=－1代入抛物线解析式即可求出，最后求出增加的宽度即可.
试题解析：
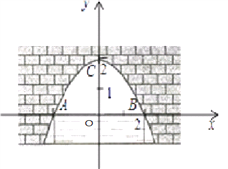
建立平面直角坐标系，设横轴x通过AB，纵轴y通过AB中点O且通过C点，
∵OC=2，
∴顶点C坐标为（0，2），
∴设抛物线解析式为y=ax2+2，
将 A点坐标（－2，0）代入解析式，得：a=－0.5，
∴抛物线解析式为：y=－0.5x2+2，
令y=－1，－1=－0.5x2+2，
解得：x=±
，
∴水面宽度增加到2
米，
比原先的宽度当然是增加了（2
－4）米．
阳光课堂课时作业系列答案科目：初中数学 来源： 题型：
【题目】把一张对面互相平行的纸条折成如图所示，EF是折痕，若∠EFB=32°，则下列结论不正确的有（ ）．
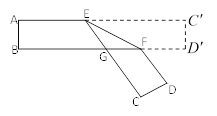
A.
B.∠AEC=148°C.∠BGE=64°D.∠BFD=116°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】图中是一副三角板，45°的三角板 Rt△DEF 的直角顶点 D 恰好在 30°的三角板 Rt△ABC 斜边 AB 的中点处，∠A＝30°，∠E＝45°，∠EDF＝∠ACB＝90°，DE 交 AC 于点 G，GM⊥AB 于 M．
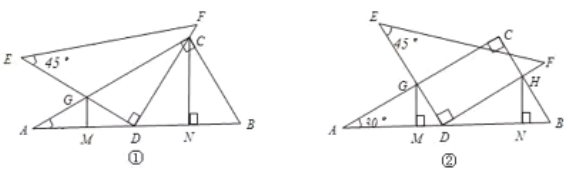
（1）如图①，当 DF 经过点 C 时，作 CN⊥AB 于 N，求证：AM＝DN；
（2）如图②，当 DF∥AC 时，DF 交 BC 于 H，作 HN⊥AB 于 N，（1）的结论仍然成立，请你说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（14分）如图，在平面直角坐标系中，矩形OCDE的三个顶点分别是C（3，0），D（3，4），E（0，4）．点A在DE上，以A为顶点的抛物线过点C，且对称轴x=1交x轴于点B．连接EC，AC．点P，Q为动点，设运动时间为t秒．
（1）填空：点A坐标为 ；抛物线的解析式为 ．
（2）在图①中，若点P在线段OC上从点O向点C以1个单位/秒的速度运动，同时，点Q在线段CE上从点C向点E以2个单位/秒的速度运动，当一个点到达终点时，另一个点随之停止运动．当t为何值时，△PCQ为直角三角形？
（3）在图②中，若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动，过点P做PF⊥AB，交AC于点F，过点F作FG⊥AD于点G，交抛物线于点Q，连接AQ，CQ．当t为何值时，△ACQ的面积最大？最大值是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
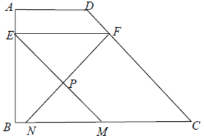
【题目】如图，E，F是正方形ABCD的边AD上两个动点，满足AE＝DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为1，则线段DH长度的最小值是_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在梯形
中，
，
，
，
，
，点E、F分别在边
、
上，
，点P与
在直线
的两侧，
，
，射线
、
与边
分别相交于点M、N，设
，
．
（1）求边的长；
（2）如图，当点P在梯形内部时，求关于x的函数解析式，并写出定义域；
（3）如果
的长为2，求梯形
的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
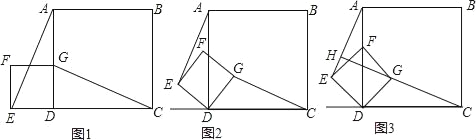
【题目】（1）如图1，正方形ABCD和正方形DEFG，G在AD边上，E在CD的延长线上．求证：AE=CG，AE⊥CG；
（2）如图2，若将图1中的正方形DEFG绕点D顺时针旋转角度θ（0°＜θ＜90°），此时AE=CG还成立吗？若成立，请给予证明；若不成立，请说明理由；
（3）如图3，当正方形DEFG绕点D顺时针旋转45°时，延长CG交AE于点H，当AD=4，DG=
时，求线段CH的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
