
【题目】在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点E、F分别在边
,点E、F分别在边![]() 、
、![]() 上,
上,![]() ,点P与
,点P与![]() 在直线
在直线![]() 的两侧,
的两侧,![]() ,
,![]() ,射线
,射线![]() 、
、![]() 与边
与边![]() 分别相交于点M、N,设
分别相交于点M、N,设![]() ,
,![]() .
.
(1)求边![]() 的长;
的长;
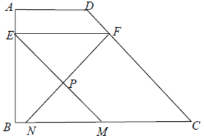
(2)如图,当点P在梯形![]() 内部时,求关于x的函数解析式,并写出定义域;
内部时,求关于x的函数解析式,并写出定义域;
(3)如果![]() 的长为2,求梯形
的长为2,求梯形![]() 的面积.
的面积.
【答案】(1)6;(2)y=-3x+10(1≤x<![]() );(2)
);(2)![]() 或32
或32
【解析】
(1)如下图,利用等腰直角三角形DHC可得到HC的长度,从而得出HB的长,进而得出AD的长;
(2)如下图,利用等腰直角三角形的性质,可得PQ、PR的长,然后利用EB=PQ+PR得去x、y的函数关系,最后根据图形特点得出取值范围;
(3)存在2种情况,一种是点P在梯形内,一种是在梯形外,分别根y的值求出x的值,然后根据梯形面积求解即可.
(1)如下图,过点D作BC的垂线,交BC于点H

∵∠C=45°,DH⊥BC
∴△DHC是等腰直角三角形
∵四边形ABCD是梯形,∠B=90°
∴四边形ABHD是矩形,∴DH=AB=8
∴HC=8
∴BH=BC-HC=6
∴AD=6
(2)如下图,过点P作EF的垂线,交EF于点Q,反向延长交BC于点R,DH与EF交于点G

∵EF∥AD,∴EF∥BC
∴∠EFP=∠C=45°
∵EP⊥PF
∴△EPF是等腰直角三角形
同理,还可得△NPM和△DGF也是等腰直角三角形
∵AE=x
∴DG=x=GF,∴EF=AD+GF=6+x
∵PQ⊥EF,∴PQ=QE=QF
∴PQ=![]()
同理,PR=![]()
∵AB=8,∴EB=8-x
∵EB=QR
∴8-x=![]()
化简得:y=-3x+10
∵y>0,∴x<![]()
当点N与点B重合时,x可取得最小值
则BC=NM+MC=NM+EF=-3x+10+![]() ,解得x=1
,解得x=1
∴1≤x<![]()
(3)情况一:点P在梯形ABCD内,即(2)中的图形
∵MN=2,即y=2,代入(2)中的关系式可得:x=![]() =AE
=AE
∴![]()
情况二:点P在梯形ABCD外,图形如下:

与(2)相同,可得y=3x-10
则当y=2时,x=4,即AE=4
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,一个点从原点O出发,按向右→向上→向右→向下的顺序依次不断移动,每次移动1个单位,其移动路线如图所示,第1次移到点A1,第二次移到点A2,第三次移到点A3,…,第n次移到点An,则点A2019的坐标是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把![]() 按下列要求进行操作:若指数为奇数则乘以
按下列要求进行操作:若指数为奇数则乘以![]() ,若指数为偶数则把它的指数除以2,如此继续下去,则第几次操作时
,若指数为偶数则把它的指数除以2,如此继续下去,则第几次操作时![]() 的指数为4?第10次操作时
的指数为4?第10次操作时![]() 的指数是多少?你有什么发现?
的指数是多少?你有什么发现?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B出发,沿轨道到达C处,在AC上,甲的速度是乙的速度的1.5倍,设t分后甲、乙两遥控车与B处的距离分别为d1,d2(单位:米),则d1,d2与t的函数关系如图,试根据图象解决下列问题.

(1)填空:乙的速度v2=________米/分;
(2)写出d1与t的函数表达式;
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探究什么时间两遥控车的信号不会产生相互干扰?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2,对角线AC、BD交于点O,∠AOD=120°,E为BD上任意点,P为AE中点,则PO+PB的最小值为 ( )

A.![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
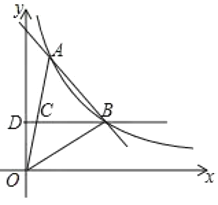
【题目】如图,一次函数y=ax+b与反比例函数y=![]() (x>0)的图像在第一象限交于A、B两点,点B坐标为(4,2),连接OA、OB,过点B作BD⊥y轴,垂足为D,交OA于点C,且OC=CA.
(x>0)的图像在第一象限交于A、B两点,点B坐标为(4,2),连接OA、OB,过点B作BD⊥y轴,垂足为D,交OA于点C,且OC=CA.
(1)求反比例函数和一次函数的表达式;
(2)根据图像直接说出不等式ax+b-![]() <0的解集为______;
<0的解集为______;
(3)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com