
【题目】公历3月12日是植树节,为宣传保护数目,激发人们爱林造林的热情,政府投资13万元给某村民小组用于购买与种植![]() 两种树苗共3000棵,完成这项种植后,剩余的款项作为村民小组的纯收入,已知用160元购买
两种树苗共3000棵,完成这项种植后,剩余的款项作为村民小组的纯收入,已知用160元购买![]() 树苗比购买
树苗比购买![]() 树苗多3棵,这两种树苗的单价、成活率及移栽费用见下表:
树苗多3棵,这两种树苗的单价、成活率及移栽费用见下表:
(1)求表中![]() 的值;
的值;
(2)设购买![]() 树苗
树苗![]() 棵,其它购买的是
棵,其它购买的是![]() 树苗,把这些树苗种植完成后,村民小组获得的纯收入为
树苗,把这些树苗种植完成后,村民小组获得的纯收入为![]() 元,请你写出
元,请你写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若要求这批树苗种植后,成活率达到93%以上(包含93%),则最多种植![]() 树苗多少棵?此时,村民小组在这项工作中,所得的纯收入最大值可以是多少元?
树苗多少棵?此时,村民小组在这项工作中,所得的纯收入最大值可以是多少元?
树苗品种 |
|
|
购买价格(元/棵) |
|
|
树苗成活率 | 90% | 95% |
移栽费用(元/棵) | 3 | 5 |
【答案】(1)![]() ;(2)
;(2)![]() ;(3)最多种植
;(3)最多种植![]() 树苗1200棵,纯收入最大值是35800元
树苗1200棵,纯收入最大值是35800元
【解析】
(1)根据题意列出方程解答即可;
(2)根据题意列出函数解析式即可;
(3)设种植![]() 树苗
树苗![]() 棵,列出解析式增函数的性质解答即可.
棵,列出解析式增函数的性质解答即可.
解:(1)根据题意,得:![]() ,
,
解得:![]() ,
,![]() ,
,
经检验,它们都是原方程的解,
但![]() 不合题意,舍去,
不合题意,舍去,
所以![]() ;
;
(2)由(1)可知:![]() 树苗购买价格:20元/棵;
树苗购买价格:20元/棵;![]() 树苗购买价格:32元/棵,根据题意,
树苗购买价格:32元/棵,根据题意,
得:![]() ,
,
即:![]() 与
与![]() 之间的函数关系式是:
之间的函数关系式是:![]() ,
,
(3)设种植![]() 树苗
树苗![]() 棵,则有:
棵,则有:![]() ,
,
解得:![]() ,
,
由(2)可知:![]() ,其中
,其中![]() ,对于此一次函数,当
,对于此一次函数,当![]() 取最大值时,纯收入
取最大值时,纯收入![]() 的值最大.
的值最大.
所以有:![]() 最大值
最大值![]() (元),
(元),
因此:最多种植![]() 树苗1200棵,纯收入最大值是35800元.
树苗1200棵,纯收入最大值是35800元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.
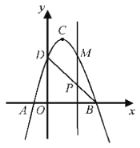
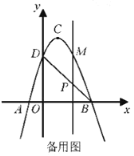
(1)求二次函数的解析式和直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴垂线,交抛物线于点
轴垂线,交抛物线于点![]() ,当点
,当点![]() 在第一象限时,求线段
在第一象限时,求线段![]() 长度的最大值;
长度的最大值;
(3)在抛物线上是否存在异于![]() 、
、![]() 的点
的点![]() ,使
,使![]() 中
中![]() 边上的高
边上的高![]() ?若存在求出点
?若存在求出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的道路AB上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,假设他们分别以不同的速度匀速行驶,甲先出发6分钟后,乙才出发,乙的速度为![]() 千米/分,在整个过程中,甲、乙两人之间的距离y(千米)与甲出发的时间x(分)之间的部分函数图象如图.
千米/分,在整个过程中,甲、乙两人之间的距离y(千米)与甲出发的时间x(分)之间的部分函数图象如图.
(1)A、B两地相距____千米,甲的速度为____千米/分;
(2)求线段EF所表示的y与x之间的函数表达式;
(3)当乙到达终点A时,甲还需多少分钟到达终点B?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价(元/件) | 40 | 90 |
售价(元/件) | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
(Ⅰ)写出y关于x的函数关系式;
(Ⅱ)该商场计划最多投入8000元用于购买这两种商品,
①至少要购进多少件甲商品?
②若销售完这些商品,则商场可获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接![]() 年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为
年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为![]() 运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的
运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的![]() 倍,并且在独立完成面积为
倍,并且在独立完成面积为![]() 的改造时,甲队比乙队少用
的改造时,甲队比乙队少用![]() 天.
天.
(1)求甲、乙两工程队每天能完成塑胶改造的面积;
(2)设甲工程队施工![]() 天,乙工程队施工
天,乙工程队施工![]() 天,刚好完成改造任务,求
天,刚好完成改造任务,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(3)若甲队每天改造费用是![]() 万元,乙队每天改造费用是
万元,乙队每天改造费用是![]() 万元,且甲、乙两队施工的总天数不超过
万元,且甲、乙两队施工的总天数不超过![]() 天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点……第n行有n个点……则下列说法:①10是三角点阵中前4行的点数和;②300是三角点阵中前24行的点数和;③前n个点数和为200的点,在这个三角点阵中位于第20行第10个点,其中正确的个数是( )

A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
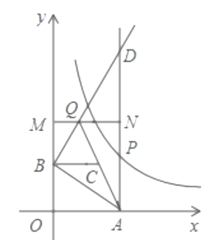
【题目】如图,在平面直角坐标系中,点A(a,0)是x轴正半轴上一点,PA⊥x轴,点B坐标为(0,b)(b>0),动点M在y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.
(1)若a=2b,点D坐标为(m,n),求![]() 的值;
的值;
(2)当点Q在线段BD上时,若四边形BQNC是菱形,面积为![]() ,求经过点B,Q两点的直线解析式;
,求经过点B,Q两点的直线解析式;
(3)当点Q在射线BD上时,且a3,b1,若以点B,C,N,Q为顶点的四边形是平行四边形,求这个平行四边形的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com