
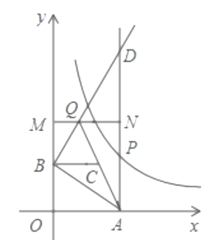
【题目】如图,在平面直角坐标系中,点A(a,0)是x轴正半轴上一点,PA⊥x轴,点B坐标为(0,b)(b>0),动点M在y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.
(1)若a=2b,点D坐标为(m,n),求![]() 的值;
的值;
(2)当点Q在线段BD上时,若四边形BQNC是菱形,面积为![]() ,求经过点B,Q两点的直线解析式;
,求经过点B,Q两点的直线解析式;
(3)当点Q在射线BD上时,且a3,b1,若以点B,C,N,Q为顶点的四边形是平行四边形,求这个平行四边形的周长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)证明![]() 得
得![]() ,从而得
,从而得![]() ,
,![]() ,故可得m,n的值,进一步可得
,故可得m,n的值,进一步可得![]() 的值;
的值;
(2)由菱形的性质可证明![]() 结合菱形BQNC的面积求出点B、D的坐标,设出直线BD的解析式,将B、D点的坐标代入解析式从而求解即可,
结合菱形BQNC的面积求出点B、D的坐标,设出直线BD的解析式,将B、D点的坐标代入解析式从而求解即可,
(3)分两类进行讨论,当点Q在线段BD上,根据题干条件求出AQ的长,进而求出四边形的周长,当点Q在线段BD的延长线上,依然根据题干条件求出AQ的长,再进一步求出四边形的周长.
(1)![]() ,
,![]() 轴
轴
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,
![]() ,
,![]()
![]()
(2)如图,
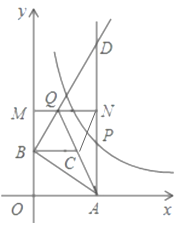
![]() 四边形
四边形![]() 是菱形,
是菱形,
![]() ,
,![]() .
.
![]() ,
,![]() 是
是![]() 的中点,
的中点,
![]() .
.
![]() ,
,![]() .
.
在![]() 和
和![]() 中,
中,
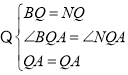 ,
,
![]() .
.
![]()
![]() .
.
![]() 四边形
四边形![]() ,
,
![]() .
.
![]() ,
,![]() ,
,![]()
![]() ,
,![]()
设经过点![]() ,
,![]() 两点的直线解析式为y=kx+b,
两点的直线解析式为y=kx+b,
把![]() ,
,![]() 代入解析式得,
代入解析式得,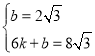 ,
,
解得,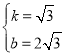
∴经过点![]() ,
,![]() 两点的直线解析式为:
两点的直线解析式为:![]()
(3)![]() ,
,![]() ,
,
![]() .
.
∵DA⊥x轴,
∴DA//y轴,
∴∠DAB=∠ABO,
又∠AOB=∠DBA
![]() ,
,
![]() .
.
![]() .
.
①如图,当点![]() 在线段
在线段![]() 上,
上,
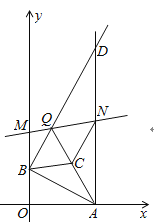
![]() ,
,![]() 为
为![]() 的中点,
的中点,
![]() .
.
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() 四边形
四边形![]() .
.
②如图,当点![]() 在线段
在线段![]() 的延长线上,
的延长线上,
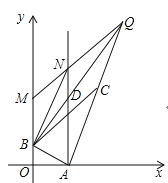
![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() .
.
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() .
.
![]() .
.
![]() .
.
![]()
![]() 平行四边形
平行四边形![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】公历3月12日是植树节,为宣传保护数目,激发人们爱林造林的热情,政府投资13万元给某村民小组用于购买与种植![]() 两种树苗共3000棵,完成这项种植后,剩余的款项作为村民小组的纯收入,已知用160元购买
两种树苗共3000棵,完成这项种植后,剩余的款项作为村民小组的纯收入,已知用160元购买![]() 树苗比购买
树苗比购买![]() 树苗多3棵,这两种树苗的单价、成活率及移栽费用见下表:
树苗多3棵,这两种树苗的单价、成活率及移栽费用见下表:
(1)求表中![]() 的值;
的值;
(2)设购买![]() 树苗
树苗![]() 棵,其它购买的是
棵,其它购买的是![]() 树苗,把这些树苗种植完成后,村民小组获得的纯收入为
树苗,把这些树苗种植完成后,村民小组获得的纯收入为![]() 元,请你写出
元,请你写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若要求这批树苗种植后,成活率达到93%以上(包含93%),则最多种植![]() 树苗多少棵?此时,村民小组在这项工作中,所得的纯收入最大值可以是多少元?
树苗多少棵?此时,村民小组在这项工作中,所得的纯收入最大值可以是多少元?
树苗品种 |
|
|
购买价格(元/棵) |
|
|
树苗成活率 | 90% | 95% |
移栽费用(元/棵) | 3 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统汁图,请根据图中信息解答下列问题:

(l)本次抽取样本容量为____,扇形统计图中A类所对的圆心角是____度;
(2)请补全统计图;
(3)若该校九年级男生有300名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
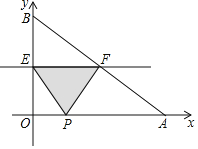
【题目】如图,在平面直角坐标系中,A、B两点的坐标分别为(20,0)和(0,15),动点P从点A出发在线段AO上以每秒2cm的速度向原点O运动,动直线EF从x轴开始以每秒lcm的速度向上平行移动(即EF∥x轴),分别与y轴、线段AB交于点E、F,连接EP、FP,设动点P与动直线EF同时出发,运动时间为t秒.
(1)求t=9时,△PEF的面积;
(2)直线EF、点P在运动过程中,是否存在这样的t使得△PEF的面积等于40cm2?若存在,请求出此时t的值;若不存在,请说明理由;
(3)当t为何值时,△EOP与△BOA相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,已知正方形ABCD的边长是4,M在DC上,M是CD的中点,点P是AC边上的一动点,则当DP+MP的值最小时,在备用图(答题卷上)中用尺规作出点P的位置,并直接写出DP的长是?
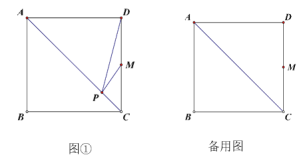
(2)如图②,已知正方形ABCD的边长是4,点M是DC上的一个动点,连结AM,作BP⊥AM于点P,连结DP,当DP最小时,在备用图(答题卷上)中用尺规作出点P的位置,并直接写出DP的长是?
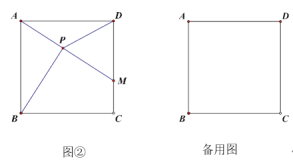
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明与小亮两个人打算骑共享单车骑行出游,两人打开手机APP进行选择,已知附近共有3种品牌的5辆车,其中A品牌与B品牌各有2辆,C品牌有1辆,手机上无法识别品牌,且有人选中车后其他人无法再选.
(1)若小明首先选择,则小明选中A品牌单车的概率为 ;
(2)求小明和小亮选中同一品牌单车的概率.(请用“画树状图”或“列表”的方法给出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 过点
过点![]() ,
,![]() ,点
,点![]() 为直线
为直线![]() 下方抛物线上一动点,
下方抛物线上一动点,![]() 为抛物线顶点,抛物线对称轴与直线
为抛物线顶点,抛物线对称轴与直线![]() 交于点
交于点![]() .
.
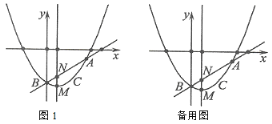
(1)求抛物线的表达式与顶点![]() 的坐标;
的坐标;
(2)在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,若存在,请求出
为顶点的四边形是平行四边形,若存在,请求出![]() 点坐标;
点坐标;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
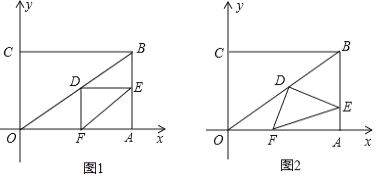
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC,连接OB,点D为OB的中点,点E是线段AB上的动点,连接DE,作DF⊥DE,交OA于点F,连接EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.
(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,![]() 的大小是否发生变化?如果变化,请说明理由;如果不变,请求出
的大小是否发生变化?如果变化,请说明理由;如果不变,请求出![]() 的值.
的值.
(3)连接AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com