
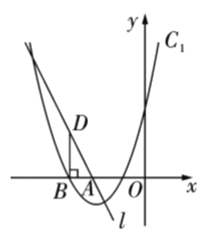
【题目】如图1,抛物线![]() 过点
过点![]() ,
,![]() ,点
,点![]() 为直线
为直线![]() 下方抛物线上一动点,
下方抛物线上一动点,![]() 为抛物线顶点,抛物线对称轴与直线
为抛物线顶点,抛物线对称轴与直线![]() 交于点
交于点![]() .
.
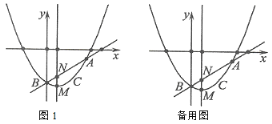
(1)求抛物线的表达式与顶点![]() 的坐标;
的坐标;
(2)在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,若存在,请求出
为顶点的四边形是平行四边形,若存在,请求出![]() 点坐标;
点坐标;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() 点的坐标为(1,-4);(2)符合条件的
点的坐标为(1,-4);(2)符合条件的![]() 点的坐标为
点的坐标为![]() ,
,![]() ;(3)
;(3)![]() 点的坐标为
点的坐标为![]() 或
或![]() .
.
【解析】
(1)![]() ,
,![]() 代入抛物线
代入抛物线![]() 即可求出抛物线解析式,配方即可求出顶点坐标;
即可求出抛物线解析式,配方即可求出顶点坐标;
(2)用待定系数法求出直线![]() 的表达式为
的表达式为![]() ,求得MN=1,分①若
,求得MN=1,分①若![]() 为平行四边形的一边,则有
为平行四边形的一边,则有![]() ,且
,且![]() 及②若
及②若![]() 为平行四边形的对角线,进行解答即可;
为平行四边形的对角线,进行解答即可;
(3)构造![]() ,使得
,使得![]() ,作
,作![]() 轴,则
轴,则![]() ,根据勾股定理可得
,根据勾股定理可得![]() ,即可求出
,即可求出![]() 点的坐标
点的坐标
(1)把![]() ,
,![]() 代入抛物线
代入抛物线![]() 得
得

解得:
∴![]()
∵![]()
∴![]() 点的坐标为(1,-4).
点的坐标为(1,-4).
(2)设直线![]() 的表达式为
的表达式为![]() ,则
,则
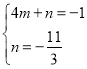
解得: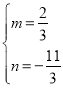
∴直线![]() 的表达式为
的表达式为![]() .
.
当![]() 时,
时,![]() ,
,
∴![]() 点的坐标为(1,-3),
点的坐标为(1,-3),
∴![]() .
.
①若![]() 为平行四边形的一边,则有
为平行四边形的一边,则有![]() ,且
,且![]() .
.
设![]() 点坐标
点坐标![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() (舍去),
(舍去),![]() .
.
∴![]() 点坐标为
点坐标为![]() .
.
②若![]() 为平行四边形的对角线,设
为平行四边形的对角线,设![]() ,则
,则![]() .
.
代入抛物线得:![]() ,解得
,解得![]() (舍去),
(舍去),![]() ,
,
∴![]()
综上所述,符合条件的![]() 点的坐标为
点的坐标为![]() ,
,![]() .
.
(3)
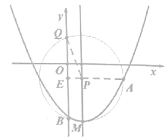
如图,在对称轴上取点![]() ,易得
,易得![]() ,且
,且![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作圆交
为半径作圆交![]() 轴与点
轴与点![]() ,则
,则![]() .作
.作![]() 轴,则
轴,则![]() ,
,
又∵![]() ,
,
∴![]()
∴![]() 点的坐标为
点的坐标为![]() 或
或![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 与
与![]() 轴的一个交点为
轴的一个交点为![]() (点
(点![]() 在点
在点![]() 的左侧),过点
的左侧),过点![]() 作
作![]() 垂直
垂直![]() 轴交直线
轴交直线![]() 于点
于点![]() .
.
(1)求抛物线的函数表达式;
(2)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]()
①求点![]() 的坐标;
的坐标;
②将拋物线![]() 向右平移使它经过点
向右平移使它经过点![]() ,此时得到的抛物线记为
,此时得到的抛物线记为![]() ,求出抛物线
,求出抛物线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
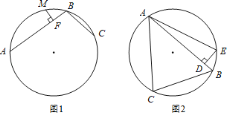
【题目】定义:圆中有公共端点的两条弦组成的折线称为圆的一条折弦.阿基米德折弦定理:如图1,AB和BC组成圆的折弦,AB>BC,M是弧ABC的中点,MF⊥AB于F,则AF=FB+BC.
如图2,△ABC中,∠ABC=60°,AB=8,BC=6,D是AB上一点,BD=1,作DE⊥AB交△ABC的外接圆于E,连接EA,则∠EAC=_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
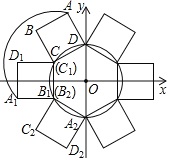
【题目】如图,⊙O的半径为2,圆心O在坐标原点,正方形ABCD的边长为2,点A、B在第二象限,点C、D在⊙O上,且点D的坐标为(0,2),现将正方形ABCD绕点C按逆时针方向旋转150°,点B运动到了⊙O上点B1处,点A、D分别运动到了点A1、D1处,即得到正方形A1B1C1D1(点C1与C重合);再将正方形A1B1C1D1绕点B1按逆时针方向旋转150°,点A1运动到了⊙O上点A2处,点D1、C1分别运动到了点D2、C2处,即得到正方形A2B2C2D2(点B2与B1重合),…,按上述方法旋转2020次后,点A2020的坐标为( )
A.(0,2)B.(2+![]() ,﹣1)
,﹣1)
C.(﹣1﹣![]() ,﹣1﹣
,﹣1﹣![]() )D.(1,﹣2﹣
)D.(1,﹣2﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
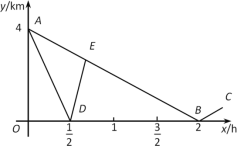
【题目】某中学九年级学生步行到郊外春游.一班的学生组成前队,速度为4km/h ,二班的学生组成后队,速度为6km/h .前队出发1h 后,后队才出发,同时,后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12km/h.若不计队伍的长度,如图,折线ABC ,A-B-C 分别表示后队,联络员在行进过程中,离前队的路程 与后队行进时间x(h) 之间的部分函数图象.
(1) 求线段AB 对应的函数关系式;
(2) 求点E 的坐标,并说明它的实际意义;
(3) 联络员从出发到他折返后第一次与后队相遇的过程中,当x 为何值时,他离前队的路程与他离后队的路程相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
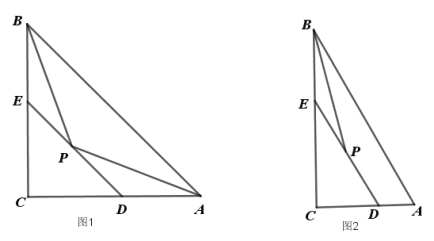
【题目】(1)如图1.在Rt△ABC中,∠C=90°,AC=BC,AP、BP分别平分∠CAB、∠CBA,过点P作DE∥AB交AC于点D,交BC于点E.求证:①点P是线段DE的中点;②求证:BP2=BE·BA;
(2)如图2.在Rt△ABC中,∠C=90°,AB=13,BC=12,BP平分∠ABC,过点P作DE∥AB交AC于点D,交BC于点E,若点P为线段DE的中点,求AD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)若这种冰箱的售价降低50元,每天的利润是 元;
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到更多的实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时利润最高,并求出最高利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com