
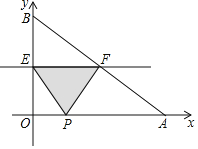
【题目】如图,在平面直角坐标系中,A、B两点的坐标分别为(20,0)和(0,15),动点P从点A出发在线段AO上以每秒2cm的速度向原点O运动,动直线EF从x轴开始以每秒lcm的速度向上平行移动(即EF∥x轴),分别与y轴、线段AB交于点E、F,连接EP、FP,设动点P与动直线EF同时出发,运动时间为t秒.
(1)求t=9时,△PEF的面积;
(2)直线EF、点P在运动过程中,是否存在这样的t使得△PEF的面积等于40cm2?若存在,请求出此时t的值;若不存在,请说明理由;
(3)当t为何值时,△EOP与△BOA相似.
【答案】(1)36cm2;(2)不存在;(3)t=6或t=![]() .
.
【解析】
(1)由于EF∥x轴,则S△PEF=![]() EFOE.t=9时,OE=9,关键是求EF.易证△BEF∽△BOA,则
EFOE.t=9时,OE=9,关键是求EF.易证△BEF∽△BOA,则![]() =
=![]() ,从而求出EF的长度,得出△PEF的面积;
,从而求出EF的长度,得出△PEF的面积;
(2)假设存在这样的t,使得△PEF的面积等于40cm2,则根据面积公式列出方程,由根的判别式进行判断,得出结论;
(3)如果△EOP与△BOA相似,由于∠EOP=∠BOA=90°,则只能点O与点O对应,然后分两种情况分别讨论:①点P与点A对应;②点P与点B对应.
解:(1)∵EF∥OA,
∴∠BEF=∠BOA
又∵∠B=∠B,
∴△BEF∽△BOA,
∴![]() =
=![]() ,
,
当t=9时,OE=9,OA=20,OB=15,
∴EF=![]() =8,
=8,
∴S△PEF=![]() EFOE=
EFOE=![]() ×8×9=36(cm2);
×8×9=36(cm2);
(2)∵△BEF∽△BOA,
∴EF=![]() =
=![]() =
=![]() (15-t),
(15-t),
∴![]() ×
×![]() (15-t)×t=40,
(15-t)×t=40,
整理,得t2-15t+60=0,
∵△=152-4×1×60<0,
∴方程没有实数根.
∴不存在使得△PEF的面积等于40cm2的t值;
(3)当∠EPO=∠BAO时,△EOP∽△BOA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得t=6;
当∠EPO=∠ABO时,△EOP∽△AOB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得t=![]() .
.
∴当t=6或t=![]() 时,△EOP与△BOA相似.
时,△EOP与△BOA相似.


科目:初中数学 来源: 题型:
【题目】尺规作图要求:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;
Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.
如图是按上述要求排乱顺序的尺规作图:

则正确的配对是( )
A. ①﹣Ⅳ,②﹣Ⅱ,③﹣Ⅰ,④﹣Ⅲ B. ①﹣Ⅳ,②﹣Ⅲ,③﹣Ⅱ,④﹣Ⅰ
C. ①﹣Ⅱ,②﹣Ⅳ,③﹣Ⅲ,④﹣Ⅰ D. ①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在线段![]() 上有一点
上有一点![]() ,在
,在![]() 的同侧作等腰
的同侧作等腰![]() 和等腰
和等腰![]() ,且
,且![]() ,
,![]() ,
,![]() ,直线
,直线![]() 与线段
与线段![]() ,线段
,线段![]() 分别交于点
分别交于点![]() ,对于下列结论:①
,对于下列结论:①![]() ∽
∽![]() ;②
;②![]() ∽
∽![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() .其中正确的是( )
.其中正确的是( )
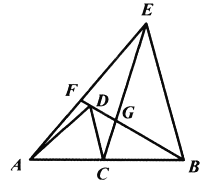
A. ①②③④B. ①②③C. ①③④D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
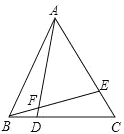
【题目】如图,△ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F,
(1)证明:△ABD≌△BCE;
(2)证明:△ABE∽△FAE;
(3)若AF=7,DF=1,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
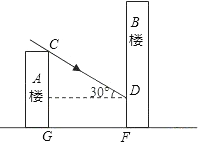
【题目】如图所示,小明家住在30米高的A楼里,小丽家住在B楼里,B楼坐落在A楼的正北面,已知当地冬至中午12时太阳光线与水平面的夹角为30°.
(1)如果A、B两楼相距16![]() 米,那么A楼落在B楼上的影子有多长?
米,那么A楼落在B楼上的影子有多长?
(2)如果A楼的影子刚好不落在B楼上,那么两楼的距离应是多少米?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随若移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A .和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调査,得到如下图表(部分信息未给出):

根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中![]() 的值,并补全条形统计图;
的值,并补全条形统计图;
(3)若该中学约有![]() 名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?
名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?
并根据以上调査结果,就中学生如何合理使用手机给出你的一条建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
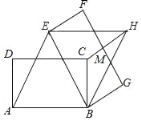
【题目】如图,矩形ABCD中,AB=6,AD=2![]() ,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM的长度为( )
,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM的长度为( )
A. ![]() B. 2 C.
B. 2 C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
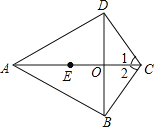
【题目】如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,点E在AO上,且OE=OC.
(1)求证:∠1=∠2;
(2)连结BE、DE,判断四边形BCDE的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com