
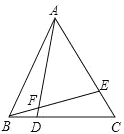
【题目】如图,△ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F,
(1)证明:△ABD≌△BCE;
(2)证明:△ABE∽△FAE;
(3)若AF=7,DF=1,求BD的长.
【答案】(1)证明见解析;(2)证明见解析;(3)BD=2![]() .
.
【解析】
(1)根据等边三角形的性质,利用SAS证得△ABD≌△BCE;
(2)由△ABD≌△BCE得∠BAD=∠CBE,又∠ABC=∠BAC,可证∠ABE=∠EAF,又∠AEF=∠BEA,由此可以证明△AEF∽△BEA;
(3)由△ABD≌△BCE得:∠BAD=∠FBD,又∠BDF=∠ADB,由此可以证明△BDF∽△ADB,然后可以得到![]() ,即BD2=ADDF=(AF+DF)DF.
,即BD2=ADDF=(AF+DF)DF.
解:(1)∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE,
在△ABD与△BCE中
∵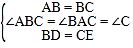 ,
,
∴△ABD≌△BCE(SAS);
(2)由(1)得:∠BAD=∠CBE,
又∵∠ABC=∠BAC,
∴∠ABE=∠EAF,
又∵∠AEF=∠BEA,
∴△AEF∽△BEA;
(3)∵∠BAD=∠CBE,∠BDA=∠FDB,
∴△ABD∽△BDF,
∴![]() ,
,
∴BD2=ADDF=(AF+DF)DF=8,
∴BD=2![]() .
.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.若四边形AC1A1C为矩形,则a,b应满足的关系式为( )
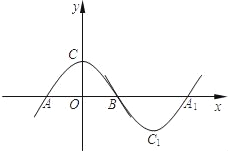
A. ab=﹣2 B. ab=﹣3 C. ab=﹣4 D. ab=﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,菱形ABCO的顶点O在坐标原点,且与反比例函数y=![]() 的图象相交于A(m,3
的图象相交于A(m,3![]() ),C两点,已知点B(2
),C两点,已知点B(2![]() ,2
,2![]() ),则k的值为( )
),则k的值为( )

A. 6B. ﹣6C. 6![]() D. ﹣6
D. ﹣6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦前夕,某企业接到一批粽子生产任务,约定这批粽子的出厂价为每只4元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,设新工人小丁第![]() 天生产的粽子数量为
天生产的粽子数量为![]() 只,
只,![]() 与
与![]() 满足如下关系:
满足如下关系:![]()
(1)小丁第几天生产的粽子数量为280只?
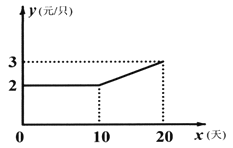
(2)如图,设第![]() 天生产的每只粽子的成本是
天生产的每只粽子的成本是![]() 元,
元,![]() 与
与![]() 之间的关系可用图中的函数图象来刻画.若小丁第
之间的关系可用图中的函数图象来刻画.若小丁第![]() 天创造的利润为
天创造的利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价-成本)
之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 朗读者
朗读者![]() 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级![]() 、
、![]() 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩![]() 满分为100分
满分为100分![]() 如图所示.
如图所示.
平均数 | 中位数 | 众数 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根据图示填写表格;
根据图示填写表格;
![]() 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
![]() 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
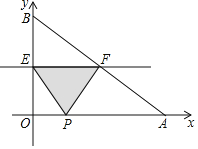
【题目】如图,在平面直角坐标系中,A、B两点的坐标分别为(20,0)和(0,15),动点P从点A出发在线段AO上以每秒2cm的速度向原点O运动,动直线EF从x轴开始以每秒lcm的速度向上平行移动(即EF∥x轴),分别与y轴、线段AB交于点E、F,连接EP、FP,设动点P与动直线EF同时出发,运动时间为t秒.
(1)求t=9时,△PEF的面积;
(2)直线EF、点P在运动过程中,是否存在这样的t使得△PEF的面积等于40cm2?若存在,请求出此时t的值;若不存在,请说明理由;
(3)当t为何值时,△EOP与△BOA相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
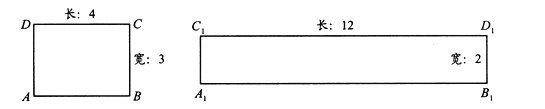
【题目】阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的2倍,则这个矩形是给定矩形的“加倍”矩形.如图,矩形![]() 是矩形
是矩形![]() 的“加倍”矩形.
的“加倍”矩形.
解决问题:
(1)当矩形的长和宽分别为3,2时,它是否存在“加倍”矩形?若存在,求出“加倍”矩形的长与宽,若不存在,请说明理由.
(2)边长为![]() 的正方形存在“加倍”正方形吗?请做出判断,并说明理由.
的正方形存在“加倍”正方形吗?请做出判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
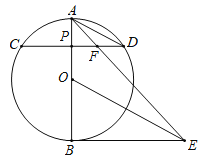
【题目】如图,AB为⊙O直径,P点为半径OA上异于O点和A点的一个点,过P点作与直径AB垂直的弦CD,连接AD,作BE⊥AB,OE∥AD交BE于E点,连接AE、DE、AE交CD于F点.
(1)求证:DE为⊙O切线;
(2)若⊙O的半径为3,sin∠ADP=![]() ,求AD;
,求AD;
(3)请猜想PF与FD的数量关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com