
【题目】已知:如图,四边形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)设![]() 的面积为
的面积为![]() ,
,![]() ,求证:S四边形ABCD
,求证:S四边形ABCD![]() .
.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)由S△AOD=S△BOC易得S△ADB=S△ACB,根据三角形面积公式得到点D和点C到AB的距离相等,则CD∥AB,于是可判断△DOC∽△BOA,然后利用相似比即可得到结论;
(2)利用相似三角形的性质可得结论.
(1)∵S△AOD=S△BOC,
∴S△AOD+S△AOB=S△BOC+S△AOB,即S△ADB=S△ACB,
∴CD∥AB,
∴△DOC∽△BOA,
∴![]() ;
;
(2)∵△DOC∽△BOA
∴![]() =k,
=k,![]() 2=k2,
2=k2,
∴DO=kOB,CO=kAO,S△COD=k2S,
∴S△AOD=kS△OAB=kS,S△COB=kS△OAB=kS,
∴S四边形ABCD=S+kS+kS+k2S=(k+1)2S.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为迎接![]() 年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为
年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为![]() 运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的
运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的![]() 倍,并且在独立完成面积为
倍,并且在独立完成面积为![]() 的改造时,甲队比乙队少用
的改造时,甲队比乙队少用![]() 天.
天.
(1)求甲、乙两工程队每天能完成塑胶改造的面积;
(2)设甲工程队施工![]() 天,乙工程队施工
天,乙工程队施工![]() 天,刚好完成改造任务,求
天,刚好完成改造任务,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(3)若甲队每天改造费用是![]() 万元,乙队每天改造费用是
万元,乙队每天改造费用是![]() 万元,且甲、乙两队施工的总天数不超过
万元,且甲、乙两队施工的总天数不超过![]() 天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,则ABCD的面积是( )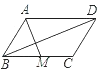
A. 30B. 36C. 54D. 72
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(a,0)是x轴正半轴上一点,PA⊥x轴,点B坐标为(0,b)(b>0),动点M在y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.
(1)若a=2b,点D坐标为(m,n),求![]() 的值;
的值;
(2)当点Q在线段BD上时,若四边形BQNC是菱形,面积为![]() ,求经过点B,Q两点的直线解析式;
,求经过点B,Q两点的直线解析式;
(3)当点Q在射线BD上时,且a3,b1,若以点B,C,N,Q为顶点的四边形是平行四边形,求这个平行四边形的周长.
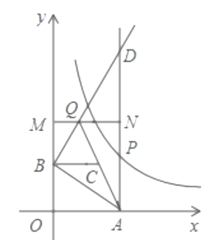
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系内,己知![]() ,直线
,直线![]() 过
过![]() ,
,![]() 、
、![]() 关于
关于![]() 的对称点分别为
的对称点分别为![]() ,请利用直尺(无刻度)和圆规按下列要求作图.
,请利用直尺(无刻度)和圆规按下列要求作图.
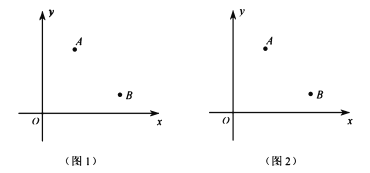
(l)当![]() 与
与![]() 重合时,请在图
重合时,请在图![]() 中画出点
中画出点![]() 位置,并求出
位置,并求出![]() 的值;
的值;
(2)当![]() 都落在
都落在![]() 轴上时,请在图2中画出直线
轴上时,请在图2中画出直线![]() ,并求出
,并求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年某市为创评“全国文明城市”称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.
抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
(1)该班男生“小刚被抽中”是 事件,“小悦被抽中”是 事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小悦被抽中”的概率为 ;
(2)试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小惠被抽中”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
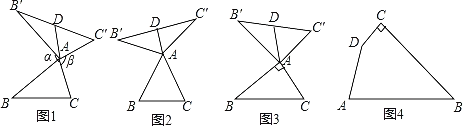
【题目】小明研究了这样一道几何题:如图1,在△ABC中,把AB点A顺时针旋转α (0°<α<180°)得到AB′,把AC绕点A逆时针旋转β得到AC′,连接B′C′.当α+β=180°时,请问△AB′C′边B′C′上的中线AD与BC的数量关系是什么?以下是他的研究过程:
特例验证:
(1)①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形ABCD,∠C=90°,∠A+∠B=120°,BC=12![]() ,CD=6,DA=6
,CD=6,DA=6![]() ,在四边形内部是否存在点P,使△PDC与△PAB之间满足小明探究的问题中的边角关系?若存在,请画出点P的位置(保留作图痕迹,不需要说明)并直接写出△PDC的边DC上的中线PQ的长度;若不存在,说明理由.
,在四边形内部是否存在点P,使△PDC与△PAB之间满足小明探究的问题中的边角关系?若存在,请画出点P的位置(保留作图痕迹,不需要说明)并直接写出△PDC的边DC上的中线PQ的长度;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
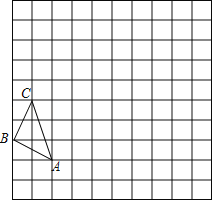
【题目】在如图的正方形网格中,每一个小正方形的边长均为1,已知格点△ABC的顶点A、C的坐标分别是(﹣2,0),(﹣3,3).
(1)请在图中的网格平面内建立平面直角坐标系.
(2)以点(﹣1,2)为位似中心,相似比为2,将△ABC放大为原来的2倍,得到△A1B1C1,画出△A1B1C1,使它与△ABC在位似中心的异侧,并写出B1点坐标为 .
(3)线段BC与线段B1C1的关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数![]() (a,b为常数,且
(a,b为常数,且![]() )与反比例函数
)与反比例函数![]() (m为常数,且
(m为常数,且![]() )的图象交于点A(﹣2,1)、B(1,n).
)的图象交于点A(﹣2,1)、B(1,n).

(1)求反比例函数和一次函数的解析式;
(2)连结OA、OB,求△AOB的面积;
(3)直接写出当![]() 时,自变量x的取值范围.
时,自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com