
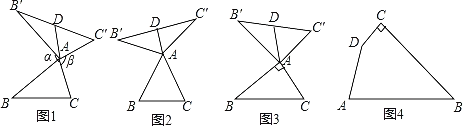
【题目】小明研究了这样一道几何题:如图1,在△ABC中,把AB点A顺时针旋转α (0°<α<180°)得到AB′,把AC绕点A逆时针旋转β得到AC′,连接B′C′.当α+β=180°时,请问△AB′C′边B′C′上的中线AD与BC的数量关系是什么?以下是他的研究过程:
特例验证:
(1)①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形ABCD,∠C=90°,∠A+∠B=120°,BC=12![]() ,CD=6,DA=6
,CD=6,DA=6![]() ,在四边形内部是否存在点P,使△PDC与△PAB之间满足小明探究的问题中的边角关系?若存在,请画出点P的位置(保留作图痕迹,不需要说明)并直接写出△PDC的边DC上的中线PQ的长度;若不存在,说明理由.
,在四边形内部是否存在点P,使△PDC与△PAB之间满足小明探究的问题中的边角关系?若存在,请画出点P的位置(保留作图痕迹,不需要说明)并直接写出△PDC的边DC上的中线PQ的长度;若不存在,说明理由.
【答案】(1)①![]() ;②4
;②4
(2) AD=![]() BC,理由见解析
BC,理由见解析
(3)存在,3![]()
【解析】
(1)①由已知条件可得AD⊥B′C′,由α+β=180°可得∠BAC+∠B′AC′=180°,已知∠BAC=60°,可求得∠B′AC′=120°继而∠B′=∠C′=30°,可得AD=![]() AB′=
AB′=![]() BC
BC
②当∠BAC=90°时,可得∠B′AC′=∠BAC=90°,△B′AC′是直角三角形,可证得△BAC≌△B′AC′,推出对应边相等,已知BC=8求出AD的长.
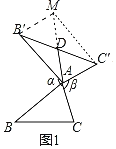
(2)先做辅助线,延长AD到M,使得AD=DM,连接B′M、C′M,如图1所示:
因为B′D=DC′,AD=DM,对角线相互平分,可得四边形AC′MB′是平行四边形,得出对应边相等,由∠BAB′+∠CAC′=180°推得∠BAC=∠AB′M,可证明△BAC≌△AB′M,所以BC=AM,AD=![]() BC;
BC;
(3)先做辅助线,作线段BC的垂直平分线交BE于P,即为点P的位置;延长AD交BC的延长线于M,线段BC的垂直平分线交BC于F,连接PA、PD、PC,作△PDC的中线PQ,连接DF交PC于O
假设P点存在,再证明理由.
根据已知角可得出△DCM是直角三角形,∠MDC=30°,可得出CM=2![]() ,DM=4
,DM=4![]() 存在;
存在;
∵CD=6,∠DCM=90°,∠MDC=30°,∠M=90°﹣∠MDC=60°,可求得EM=![]() BM=7
BM=7![]() ,DE=EM﹣DM=7
,DE=EM﹣DM=7![]() ﹣4
﹣4![]() =3
=3![]() ,
,
由已知DA=6![]() ,推得AE=DE
,推得AE=DE
且BE⊥AD,可得PF是线段BC的垂直平分线,证得PA=PD
因为PB=PC,PF∥CD,可求得CF=![]() BC=6
BC=6![]() ,利用线段长度可求得∠CDF=60°
,利用线段长度可求得∠CDF=60°
利用全等三角形判定定理可证得△FCP≌△CFD(AAS),进而证得四边形CDPF是矩形,
得∠CDP=90°,∠ADP =60°,可得△ADP是等边三角形,求出DQ、DP,在Rt△PDQ中可求得PQ长度.
(1)①∵△ABC是等边三角形
∴AB=BC=AC=AB′=AC′,∠BAC=60°
∵DB′=DC′
∴AD⊥B′C′
∵∠BAB′+∠CAC′=180°
∴∠BAC+∠B′AC′=180°
∴∠B′AC′=180°﹣∠BAC=180°﹣60°=120°
∴∠B′=∠C′=30°
∴AD=![]() AB′=
AB′=![]() BC
BC
故答案:![]()
②∵∠BAB′+∠CAC′=180°
∴∠BAC+∠B′AC′=180°
∵∠BAC=90°
∴∠B′AC′=∠BAC=90°
在△BAC和△B′AC′中,
∴△BAC≌△B′AC′(SAS)
∴BC=B′C′
∵B′D=DC′
∴AD=![]() B′C′=
B′C′=![]() BC=4
BC=4
故答案:4
(2)AD与BC的数量关系:AD=![]() BC;理由如下:
BC;理由如下:
延长AD到M,使得AD=DM,连接B′M、C′M,如图1所示:
∵B′D=DC′,AD=DM,
∴四边形AC′MB′是平行四边形,
∴∠B′AC′+∠AB′M=180°,AC′=B′M=AC,
∵∠BAB′+∠CAC′=180°,
∴∠BAC+∠B′AC′=180°,
∴∠BAC=∠AB′M,
在△BAC和△AB′M中,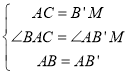 ,
,
∴△BAC≌△AB′M(SAS),
∴BC=AM,
∴AD=![]() BC;
BC;

(3)存在;作BE⊥AD于E,作线段BC的垂直平分线交BE于P,即为点P的位置;理由如下:
延长AD交BC的延长线于M,线段BC的垂直平分线交BC于F,连接PA、PD、PC,作△PDC的中线PQ,连接DF交PC于O,如图4所示:
∵∠A+∠B=120°,
∴∠ADC=150°,
∴∠MDC=30°,
在Rt△DCM中,∵CD=6,∠DCM=90°,∠MDC=30°,
∴CM=2![]() ,DM=4
,DM=4![]() ,∠M=90°﹣∠MDC=60°,
,∠M=90°﹣∠MDC=60°,
在Rt△BEM中,∵∠BEM=90°,BM=BC+CM=12![]() +2
+2![]() =14
=14![]() ,∠MBE=90°﹣∠M=30°,
,∠MBE=90°﹣∠M=30°,
∴EM=![]() BM=7
BM=7![]() ,
,
∴DE=EM﹣DM=7![]() ﹣4
﹣4![]() =3
=3![]() ,
,
∵DA=6![]() ,
,
∴AE=DE,
∵BE⊥AD,
∴PA=PD,
∵PF是线段BC的垂直平分线,
∴PB=PC,PF∥CD,
在Rt△CDF中,∵CD=6,CF=![]() BC=6
BC=6![]() ,
,
∴tan∠CDF=![]() =
=![]() =
=![]() ,
,
∴∠CDF=60°,
∴∠MDF=∠MDC+∠CDF=30°+60°=90°,
∴∠ADF=90°=∠AEB,
∴∠CBE=∠CFD,
∵∠CBE=∠PCF,
∴∠CFD=∠PCF=30°,
∵∠CFD+∠CDF=90°,∠PCF+∠CPF=90°,
∴∠CPF=∠CDF=60°,
在△FCP和△CFD中,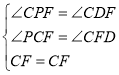 ,
,
∴△FCP≌△CFD(AAS),
∴CD=PF,
∵CD∥PF,
∴四边形CDPF是矩形,
∴∠CDP=90°,
∴∠ADP=∠ADC﹣∠CDP=60°,
∴△ADP是等边三角形,
∴∠APD=60°,
∵∠BPF=∠CPF=90°﹣30°=60°,
∴∠BPC=120°,
∴∠APD+∠BPC=180°,
∴△PDC与△PAB之间满足小明探究的问题中的边角关系;
在Rt△PDQ中,∵∠PDQ=90°,PD=DA=6![]() ,DN=
,DN=![]() CD=3,
CD=3,
∴PQ=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)如图①,已知正方形ABCD的边长是4,M在DC上,M是CD的中点,点P是AC边上的一动点,则当DP+MP的值最小时,在备用图(答题卷上)中用尺规作出点P的位置,并直接写出DP的长是?
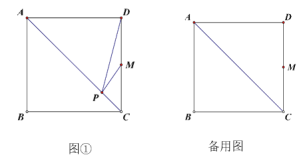
(2)如图②,已知正方形ABCD的边长是4,点M是DC上的一个动点,连结AM,作BP⊥AM于点P,连结DP,当DP最小时,在备用图(答题卷上)中用尺规作出点P的位置,并直接写出DP的长是?
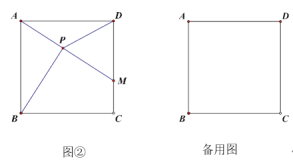
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 过点
过点![]() ,
,![]() ,点
,点![]() 为直线
为直线![]() 下方抛物线上一动点,
下方抛物线上一动点,![]() 为抛物线顶点,抛物线对称轴与直线
为抛物线顶点,抛物线对称轴与直线![]() 交于点
交于点![]() .
.
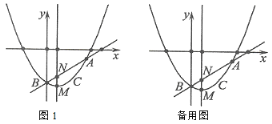
(1)求抛物线的表达式与顶点![]() 的坐标;
的坐标;
(2)在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,若存在,请求出
为顶点的四边形是平行四边形,若存在,请求出![]() 点坐标;
点坐标;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
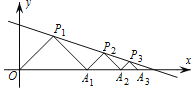
【题目】如图,在平面直角坐标系中,△P1OA1,△P2A1A2,△P3A2A3……都是等腰Rt△,直角顶点P1(3,3),P2,P3……,均在直线y=﹣![]() x+4上,设△P1OA1,△P2A1A2,△P3A2A3……的面积分别为S1,S2,S3……则S2019的值为( )
x+4上,设△P1OA1,△P2A1A2,△P3A2A3……的面积分别为S1,S2,S3……则S2019的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ACB=∠DBC,添加以下条件,不能判定△ABC≌△DCB的是( )
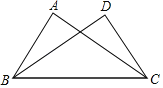
A.∠ABC=∠DCBB.∠ABD=∠DCA
C.AC=DBD.AB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与函数
与函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,且点
两点,且点![]() 的坐标为
的坐标为![]() .
.
(1)求![]() 的值;
的值;
(2)已知点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交直线
轴的直线,交直线![]() 于点
于点![]() ,交函数
,交函数![]() 的图象于点
的图象于点![]() .
.
①当![]() 时,求线段
时,求线段![]() 的长;
的长;
②若![]() ,结合函数的图象,直接写出
,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com