练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
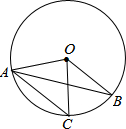
    17．如图，在⊙O中，弦AC∥半径OB，∠BOC=50°，则∠OAB的度数为（　　）
    A．25°B．50°C．60°D．30°

    分析 由圆周角定理求得∠BAC=25°，由AC∥OB，∠BAC=∠B=25°，由等边对等角得出∠OAB=∠B=25°，即可求得答案．

    解答 解：∵∠BOC=2∠BAC，∠BOC=50°，
    ∴∠BAC=25°，
    ∵AC∥OB，
    ∴∠BAC=∠B=25°，
    ∵OA=OB，
    ∴∠OAB=∠B=25°，
    故选：A．

    点评 此题考查了圆周角定理以及平行线的性质．此题难度不大，注意掌握数形结合思想的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

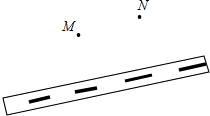    7．如图，靠近公路有两个村庄M、N，现在M村决定修建两条公路，一条与N村相连，一条与公路相连，请用图示说明这两条公路如何修建，使得费用最少（公路越短，费用越低，反之越高）并用你所学的数学知识作出图形（不必说明理由）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．某企业生产的一批产品上市后30天内全部售完，调查发现，国内市场的日销售量为y1（吨）与时间t（t为整数，单位：天）的关系如图1所示的抛物线的一部分，而国外市场的日销售量y2（吨）与时间t，t为整数，单位：天）的关系如图2所示．
    （1）求y1与时间t的函数关系式及自变量t的取值范围，并写出y2与t的函数关系式及自变量t的取值范围；
    （2）设国内、国外市场的日销售总量为y吨，直接写出y与时间t的函数关系式，当销售第几天时，国内、外市场的日销售总量最早达到75吨？
    （3）判断上市第几天国内、国外市场的日销售总量y最大，并求出此时的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知一组数据a、b、c、d的方差是2，则另一组数据2a+3、2b+3、2c+3、2d+3的方差是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，抛物线y=-x2+2x+3与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D和点C关于抛物线的对称轴对称，直线AD与y轴交于点E．

    （1）求直线AD的解析式；
    （2）如图1，直线AD上方的抛物线上有一点F，过点F作FG⊥AD于点G，作FH平行于x轴交直线AD于点H，求△FGH周长的最大值；
    （3）点M是抛物线的顶点，点P是y轴上一点，点Q是坐标平面内一点，以A，M，P，Q为顶点的四边形是以AM为边的矩形．若点T和点Q关于AM所在直线对称，求点T的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，∠A=∠D．
    （1）求证：AB=CD．
    （2）若AB=CF，∠B=30°，求∠D的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

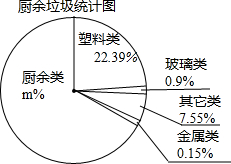    9．杭州市推行垃圾分类已经多年，但在剩余垃圾中除了厨余类垃圾还混杂着非厨余类垃圾．如图是杭州某一天收到的厨余垃圾的统计图．
    （1）试求出m的值；
    （2）杭州市某天收到厨余垃圾约200吨，请计算其中混杂着的玻璃类垃圾的吨数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图，直线l1∥l2，∠α=∠β，∠1=40°，则∠2=140°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．已知一个正比例函数的图象与一个反比例函数的一个交点坐标为（1，3），则另一个交点坐标是（-1，-3）．

    查看答案和解析>>

    同步练习册答案