
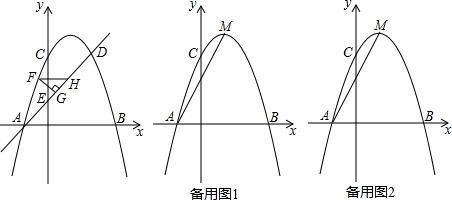
���� ��1�������C��0��3����A��-1��0����B��3��0�����������䷽����y=-��x-1��2+4���������߶Գ���Ϊֱ��x=1�����ǿ�ȷ��D��2��3����������ô���ϵ������ֱ��AD�Ľ���ʽ��
��2����E��0��1�����жϡ�OAEΪ����ֱ�������Σ����EAO=45�㣬����FH��OA����ɵõ���FGHΪ����ֱ�������Σ�����F��FN��x�ύAD��N����ͼ�����FNHΪ����ֱ�������Σ�����GH=NG�����ǵõ���FGH�ܳ����ڡ�FGN���ܳ�������FG=GN=$\frac{\sqrt{2}}{2}$FN�����FGN�ܳ�=��1+$\sqrt{2}$��FN�����Ե�FN���ʱ����FGN�ܳ��������F��x��-x2+2x+3������N��x��x+1������FN=-x2+2x+3-x-1�����ö��κ�������ֵ����ɵõ�x=$\frac{1}{2}$ʱ��FH�����ֵ$\frac{9}{4}$�����ǡ�FGN�ܳ������ֵΪ$\frac{9+9\sqrt{2}}{4}$��
��3��ֱ��AM��y����R��M��1��4�������ô���ϵ�������ֱ��AM�Ľ���ʽΪy=2x+2����R��0��2����Ȼ��������ۣ���AQΪ����AMPQ�ĶԽ��ߣ���ͼ1������Rt��AOR��Rt��POA���ɼ����OP=$\frac{1}{2}$����P������Ϊ��0��-$\frac{1}{2}$������������ƽ�ƿɵõ�Q��2��$\frac{7}{2}$���������ɵ�T�͵�Q����AM����ֱ�߶Գƣ������߶��е����깫ʽ��T������Ϊ��0��$\frac{9}{2}$������APΪ����APQM�ĶԽ��ߣ������ӳ�QA��y����S����ͼ2��ͬ���ɵ�S������Ϊ��0��-$\frac{1}{2}$������R��ΪAM���е㣬��R��ΪPS���е㣬����PM=SA��P��0��$\frac{9}{2}$��������PM=AQ����AQ=AS�����ǿ��жϵ�Q����AM�ĶԳƵ�ΪS����T������Ϊ��0��-$\frac{1}{2}$����
��� �⣺��1����x=0ʱ��y=-x2+2x+3=3����C��0��3����
��y=0ʱ��-x2+2x+3=0�����x1=-1��x2=3����A��-1��0����B��3��0����
��y=-x2+2x+3=-��x-1��2+4��
�������߶Գ���Ϊֱ��x=1��
����D�͵�C����ֱ��x=1�Գƣ�
��D��2��3����
��ֱ��AD�Ľ���ʽΪy=kx+b��
��A��-1��0����D��2��3���ֱ�����$\left\{\begin{array}{l}{-k+b=0}\\{2k+b=3}\end{array}\right.$�����$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$��
��ֱ��AD�Ľ���ʽΪy=x+1��
��2����x=0ʱ��y=x+1=1����E��0��1����
��OA=OE��
���OAEΪ����ֱ�������Σ�
���EAO=45�㣬
��FH��OA��
���FGHΪ����ֱ�������Σ�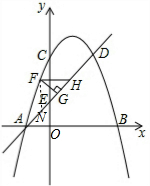 ����F��FN��x�ύAD��N����ͼ��
����F��FN��x�ύAD��N����ͼ��
��FN��FH��
���FNHΪ����ֱ�������Σ�
��FG��HN��
��GH=NG��
���FGH�ܳ����ڡ�FGN���ܳ���
��FG=GN=$\frac{\sqrt{2}}{2}$FN��
���FGN�ܳ�=��1+$\sqrt{2}$��FN��
�൱FN���ʱ����FGN�ܳ������
��F��x��-x2+2x+3������N��x��x+1����
��FN=-x2+2x+3-x-1=-��x-$\frac{1}{2}$��2+$\frac{9}{4}$��
��x=$\frac{1}{2}$ʱ��FH�����ֵ$\frac{9}{4}$��
���FGN�ܳ������ֵΪ��1+$\sqrt{2}$����$\frac{9}{4}$=$\frac{9+9\sqrt{2}}{4}$��
����FGH�ܳ������ֵΪ$\frac{9+9\sqrt{2}}{4}$��
��3��ֱ��AM��y����R��y=-x2+2x+3=-��x-1��2+4����M��1��4��
��ֱ��AM�Ľ���ʽΪy=mx+n��
��A��-1��0����M��1��4���ֱ�����$\left\{\begin{array}{l}{-m+n=0}\\{m+n=4}\end{array}\right.$�����$\left\{\begin{array}{l}{m=2}\\{n=2}\end{array}\right.$��
��ֱ��AM�Ľ���ʽΪy=2x+2��
��x=0ʱ��y=2x+2=2����R��0��2����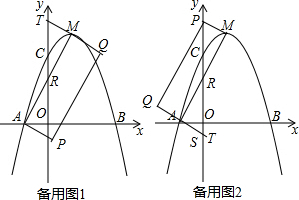 ��AQΪ����APQM�ĶԽ��ߣ���ͼ1��
��AQΪ����APQM�ĶԽ��ߣ���ͼ1��
�ߡ�RAP=90�㣬
��AO��PR��
��Rt��AOR��Rt��POA��
��AO��OP=OR��OA����1��OP=2��1�����OP=$\frac{1}{2}$��
��P��������0��-$\frac{1}{2}$����
�ߵ�A��-1��0������ƽ��4����λ������ƽ��2����λ�õ�M��1��4����
���P��0��-$\frac{1}{2}$������ƽ��4����λ������ƽ��2����λ�õ�Q��2��$\frac{7}{2}$����
�ߵ�T�͵�Q����AM����ֱ�߶Գƣ�
��T��������0��$\frac{9}{2}$����
��APΪ����AMPQ�ĶԽ��ߣ������ӳ�QA��y����S����ͼ2��
ͬ���ɵ�S������Ϊ��0��-$\frac{1}{2}$����
��R��ΪAM���е㣬
��R��ΪPS���е㣬
��PM=SA��P��0��$\frac{9}{2}$����
��PM=AQ��
��AQ=AS��
���Q����AM�ĶԳƵ�ΪS��
��T��������0��-$\frac{1}{2}$����
������������T��������0��$\frac{9}{2}$����0��-$\frac{1}{2}$����
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ��������ʡ����κ�����x��Ľ�������;��ε����ʣ������ô���ϵ������������ʽ������������������ε����ʼ����߶εij�����ס����ϵ�е�ƽ�ƵĹ��ɣ�


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ͬһƽ���ڣ�����ƽ�еĸ���l1��l2����һ����z���͵�·��ͨ������AB������ٹ�·l1��30��ǣ�CD��l2��40��Ľǣ���ABC=90�㣬���BCD�Ķ���Ϊ��������
��ͼ����ͬһƽ���ڣ�����ƽ�еĸ���l1��l2����һ����z���͵�·��ͨ������AB������ٹ�·l1��30��ǣ�CD��l2��40��Ľǣ���ABC=90�㣬���BCD�Ķ���Ϊ��������| A�� | 70�� | B�� | 90�� | C�� | 100�� | D�� | 110�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
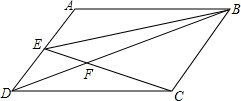 ��ͼ����?ABCD�У���E��AD�е㣮
��ͼ����?ABCD�У���E��AD�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
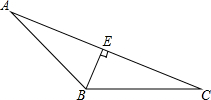 ��ͼ���ڡ�ABC�У�BE��AC��BC=5cm��AC=8cm��BE=3cm��
��ͼ���ڡ�ABC�У�BE��AC��BC=5cm��AC=8cm��BE=3cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
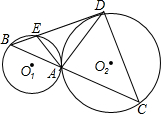 ��ͼ����֪��O1����O2�����ڵ�A������A��ֱ�߽���O1��B������O2��C������B��ֱ��BD���O1��O2�ֱ��ཻ��E��D������AE��AD��DC����AE��AD=ED��DC��
��ͼ����֪��O1����O2�����ڵ�A������A��ֱ�߽���O1��B������O2��C������B��ֱ��BD���O1��O2�ֱ��ཻ��E��D������AE��AD��DC����AE��AD=ED��DC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
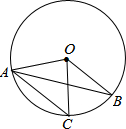 ��ͼ���ڡ�O�У���AC�ΰ뾶OB����BOC=50�㣬���OAB�Ķ���Ϊ��������
��ͼ���ڡ�O�У���AC�ΰ뾶OB����BOC=50�㣬���OAB�Ķ���Ϊ��������| A�� | 25�� | B�� | 50�� | C�� | 60�� | D�� | 30�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����֪�ڡ�O�У�AB���ң��뾶OC��AB������Ϊ��D��Ҫʹ�ı���OACBΪ���Σ�����Ҫ����һ��������������������ǣ�������
��ͼ����֪�ڡ�O�У�AB���ң��뾶OC��AB������Ϊ��D��Ҫʹ�ı���OACBΪ���Σ�����Ҫ����һ��������������������ǣ�������| A�� | AD=BD | B�� | OD=CD | C�� | ��CAD=��CBD | D�� | ��OCA=��OCB |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
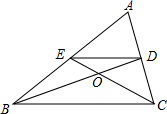 ��ͼ���ڡ�ABC�У�BD��CE�ֱ��DZ�AC��AB�ϵ����ߣ�BD��CE�ཻ�ڵ�O����$\frac{OB}{OD}$=2��
��ͼ���ڡ�ABC�У�BD��CE�ֱ��DZ�AC��AB�ϵ����ߣ�BD��CE�ཻ�ڵ�O����$\frac{OB}{OD}$=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com