
【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D. 
(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
【答案】解:(Ⅰ)如图①, 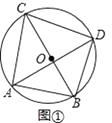
∵BC是⊙O的直径,
∴∠CAB=∠BDC=90°.
∵在直角△CAB中,BC=10,AB=6,
∴由勾股定理得到:AC= ![]() =
= ![]() =8.
=8.
∵AD平分∠CAB,
∴ ![]() =
= ![]() ,
,
∴CD=BD.
在直角△BDC中,BC=10,CD2+BD2=BC2 ,
∴易求BD=CD=5 ![]() ;
;
(Ⅱ)如图②,连接OB,OD.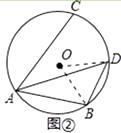
∵AD平分∠CAB,且∠CAB=60°,
∴∠DAB= ![]() ∠CAB=30°,
∠CAB=30°,
∴∠DOB=2∠DAB=60°.
又∵OB=OD,
∴△OBD是等边三角形,
∴BD=OB=OD.
∵⊙O的直径为10,则OB=5,
∴BD=5.
【解析】(Ⅰ)利用圆周角定理可以判定△CAB和△DCB是直角三角形,利用勾股定理可以求得AC的长度;利用圆心角、弧、弦的关系推知△DCB也是等腰三角形,所以利用勾股定理同样得到BD=CD=5 ![]() ;(Ⅱ)如图②,连接OB,OD.由圆周角定理、角平分线的性质以及等边三角形的判定推知△OBD是等边三角形,则BD=OB=OD=5.
;(Ⅱ)如图②,连接OB,OD.由圆周角定理、角平分线的性质以及等边三角形的判定推知△OBD是等边三角形,则BD=OB=OD=5.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留半小时后返回A地.如图是他们离A地的距离y(千米)与时间x(时)之间的函数关系图象.
(1)求甲从B地返回A地的过程中,y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若乙出发后2小时和甲相遇,求乙从A地到B地用了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“幸”、“福”、“济”、“宁”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“福”的概率为多少?
(2)小颖从中任取一球,记下汉字后放回袋中,然后再从中任取一球,求小颖取出的两个球上汉字恰能组成“幸福”或“济宁”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是cm. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1,反比例函数y= ![]() 的图象经过A,B两点,则菱形ABCD的面积为 .
的图象经过A,B两点,则菱形ABCD的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.
(1)建立适当的平面直角坐标系,
①直接写出O、P、A三点坐标;
②求抛物线L的解析式;
(2)求△OAE与△OCE面积之和的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数 ![]() 的图象是直线l1 , l1与x轴、y轴分别相交于A、B两点.直线l2过点C(a,0)且与直线l1垂直,其中a>0.点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位.
的图象是直线l1 , l1与x轴、y轴分别相交于A、B两点.直线l2过点C(a,0)且与直线l1垂直,其中a>0.点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位. 
(1)写出A点的坐标和AB的长;
(2)当点P、Q运动了多少秒时,以点Q为圆心,PQ为半径的⊙Q与直线l2、y轴都相切,求此时a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com