
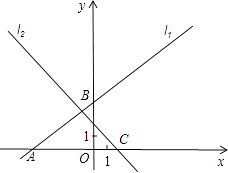
【题目】在平面直角坐标系xOy中,一次函数 ![]() 的图象是直线l1 , l1与x轴、y轴分别相交于A、B两点.直线l2过点C(a,0)且与直线l1垂直,其中a>0.点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位.
的图象是直线l1 , l1与x轴、y轴分别相交于A、B两点.直线l2过点C(a,0)且与直线l1垂直,其中a>0.点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位. 
(1)写出A点的坐标和AB的长;
(2)当点P、Q运动了多少秒时,以点Q为圆心,PQ为半径的⊙Q与直线l2、y轴都相切,求此时a的值.
【答案】
(1)解:∵一次函数 ![]() 的图象是直线l1,l1与x轴、y轴分别相交于A、B两点,
的图象是直线l1,l1与x轴、y轴分别相交于A、B两点,
∴y=0时,x=﹣4,
∴A(﹣4,0),AO=4,
∵图象与y轴交点坐标为:(0,3),BO=3,
∴AB=5
(2)解:由题意得:AP=4t,AQ=5t, ![]() =t,
=t,
又∠PAQ=∠OAB,
∴△APQ∽△AOB,
∴∠APQ=∠AOB=90°,
∵点P在l1上,
∴⊙Q在运动过程中保持与l1相切,
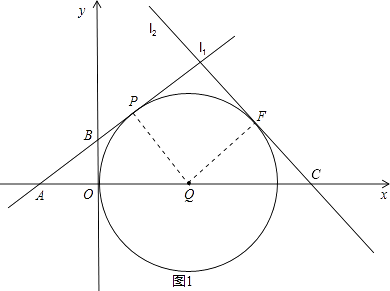
①当⊙Q在y轴右侧与y轴相切时,设l2与⊙Q相切于F,由△APQ∽△AOB,得:
∴ ![]() ,
,
∴PQ=6;
故AQ=10,则运动时间为: ![]() =2(秒);
=2(秒);
连接QF,则QF=PQ,
∵直线l2过点C(a,0)且与直线l1垂直,FQ⊥l2,
∴∠APQ=∠QFC=90°,AP∥FQ,
∴∠PAQ=∠FQC,
∴△QFC∽△APQ,
∴△QFC∽△APQ∽△AOB,
得: ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴QC= ![]() ,
,
∴a=OQ+QC=OC= ![]() ,
,
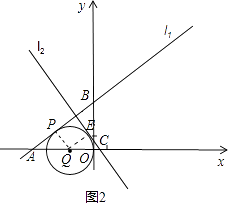
②如图2,当⊙Q在y轴的左侧与y轴相切时,设l2与⊙Q相切于E,由△APQ∽△AOB得: ![]() ,
,
∴PQ= ![]() ,
,
则AQ=4﹣ ![]() =2.5,
=2.5,
∴则运动时间为: ![]() =
= ![]() (秒);
(秒);
故当点P、Q运动了2秒或 ![]() 秒时,以点Q为圆心,PQ为半径的⊙Q与直线l2、y轴都相切,
秒时,以点Q为圆心,PQ为半径的⊙Q与直线l2、y轴都相切,
连接QE,则QE=PQ,
∵直线l2过点C(a,0)且与直线l1垂直,⊙Q在运动过程中保持与l1相切于点P,
∴∠AOB=90°,∠APQ=90°,
∵∠PAO=∠BAO,
∴△APQ∽△AOB,
同理可得:△QEC∽△APQ∽△AOB得: ![]() ,
,
∴ ![]() ,
, ![]() =
= ![]() ,
,
∴QC= ![]() ,a=QC﹣OQ=
,a=QC﹣OQ= ![]() ,
,
综上所述,a的值是: ![]() 和
和 ![]() ,
,
【解析】(1)根据一次函数图象与坐标轴的交点求法,分别求出坐标即可;(2)根据相似三角形的判定得出△APQ∽△AOB,以及当⊙Q在y轴右侧与y轴相切时,当⊙Q在y轴的左侧与y轴相切时,分别分析得出答案.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】广安某网站调查,2016年网民们最关注的热点话题分别有:消费、教育、环保、反腐及其它共五类.根据调查的部分相关数据,绘制的统计图表如下: 
根据以上信息解答下列问题:
(1)请补全条形统计图并在图中标明相应数据;
(2)若广安市约有900万人口,请你估计最关注环保问题的人数约为多少万人?
(3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,则抽取的两人恰好是甲和乙的概率是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D. 
(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.已知二次函数y=﹣x2+bx+3的图象与x轴的一个交点为A(4,0),与y轴交于点B.
(1)求此二次函数关系式和点B的坐标;
(2)在x轴的正半轴上是否存在点P.使得△PAB是以AB为底边的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个布袋都不透明,甲袋中装有1个红球和1个白球;乙袋中装有一个红球和2个白球;丙袋中装有2个白球.这些球除颜色外都相同.从这3个袋中各随机地取出1个球. (Ⅰ)取出的3个球恰好是2个红球和1个白球的概率是多少?
(Ⅱ)取出的3个球全是白球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A、B两点,与双曲线y2=![]() (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
①S△ADB=S△ADC;
②当0<x<3时,y1<y2;
③如图,当x=3时,EF=![]() ;
;
④当x>0时,y1随x的增大而增大,y2随x的增大而减小.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、4三张牌,抽取方式及规则不变,乙的方案公平吗?(只回答,不说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD于正方形A1B1C1D1关于某点中心对称,已知A,D1 , D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标.
(2)写出顶点B,C,B1 , C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=![]() x与一次函数y=﹣x+7的图象交于点A.
x与一次函数y=﹣x+7的图象交于点A.
(1)求点A的坐标。
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交y=![]() x和y=﹣x+7的图象于点B、C,连接OC.若BC=
x和y=﹣x+7的图象于点B、C,连接OC.若BC=![]() OA,求△OBC的面积.
OA,求△OBC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com