
【题目】如图,以△ABC的边BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点E.
(1)如图1,若∠ABC=90°,求证:OE∥AC;
(2)如图2,已知AB=AC,若sin∠ADE=![]() , 求tanA的值.
, 求tanA的值.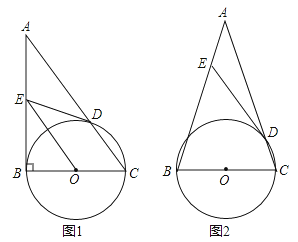
【答案】解:(1)证明:连结OD,如图1,
∵DE为⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,
在Rt△OBE和Rt△ODE中,![]()
∴Rt△OBE≌Rt△ODE,
∴∠1=∠2,
∵OC=OD,
∴∠3=∠C,
而∠1+∠2=∠C+∠3,
∴∠2=∠C,
∴OE∥AC;
(2)解:连结OD,作OF⊥CD于F,DH⊥OC于H,如图2,
∵AB=AC,OC=OD,
而∠ACB=∠OCD,
∴∠A=∠COD,
∵DE为⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,
∴∠ADE+∠ODF=90°,
而∠DOF+∠ODF=90°,
∴∠ADE=∠DOF,
∴sin∠DOF=sin∠ADE=![]() ,
,
在Rt△DOF中,sin∠DOF=![]() =
=![]() ,
,
设DF=x,则OD=3x,
∴OF=![]() =2
=2![]() x,DF=CF=x,OC=3x,
x,DF=CF=x,OC=3x,
∵![]() DHOC=
DHOC=![]() OFCD,
OFCD,
∴DH=![]() =
=![]() x,
x,
在Rt△ODH中,OH=![]() =
=![]() x,
x,
∴tan∠DOH=![]() =
=![]() =
=![]() ,
,
∴tan∠A=![]() .
.

【解析】(1)连结OD,如图1,根据切线的性质得∠ODE=90°,再证明Rt△OBE≌Rt△ODE得到∠1=∠2,加上∠3=∠C,则利用三角形外角性质可得∠2=∠C,然后根据平行线的判定可判断OE∥AC;
(2)连结OD,作OF⊥CD于F,DH⊥OC于H,如图2,根据等腰三角形的性质和三角形内角和定理,由AB=AC,OC=OD,∠ACB=∠OCD可得∠A=∠COD,根据切线的性质得∠ODE=90°,则∠ADE+∠ODF=90°,
而∠DOF+∠ODF=90°,利用等角的余角相等得∠ADE=∠DOF,于是有sin∠DOF=sin∠ADE=![]() , 在Rt△DOF中,根据正弦的定义得到
, 在Rt△DOF中,根据正弦的定义得到![]() =
=![]() , 则可设DF=x,则OD=3x,利用勾股定理计算出OF=2
, 则可设DF=x,则OD=3x,利用勾股定理计算出OF=2![]() x,DF=CF=x,OC=3x,接着可运用面积法计算出DH=
x,DF=CF=x,OC=3x,接着可运用面积法计算出DH=![]() span>x,然后在Rt△ODH中用勾股定理计算出OH=
span>x,然后在Rt△ODH中用勾股定理计算出OH=![]() x,再根据正切的定义求解即可.
x,再根据正切的定义求解即可.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B、C三地,A地在B、C两地之间.甲、乙两辆汽车分别从B、C两地同时出发,沿这条公路匀速相向行驶,分别到达目的地C、B两地后停止行驶.甲、乙两车离A地的距离y1、y2(千米)与行驶时间x(时)的函数关系如图所示.
(1)求线段MN的函数表达式;
(2)求点P的坐标,并说明点P的实际意义;
(3)在图中补上乙车从A地行驶到B地的函数图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学兴趣小组活动中,同学们做了一个找朋友的游戏:有六个同学A、B、C、D、E、F分别藏在六张大纸牌的后面,如图,A、B、C、D、E、F所持的纸牌的前面分别写有六个算式:66;63+63;(63)3;(2×62)×(3×63);(22×32)3;(64)3÷62.游戏规定:所持算式的值相等的两个人是朋友.如果现在由同学A来找他的朋友,他可以找谁呢?说说你的看法.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊数学家把数1,3,6,10,15,21,……叫做三角形数,它有一定的规律性,若把第一个三角形数记为a1 ,第二个三角数形记为a 2 ,……,第n个三角形数记为an,计算a2-a1,a 3-a2……由此推算a 100-a 99 =________;a100=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )

A. 8 B. 16 C. 24 D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB为⊙O的直径,P为AB延长线上的任意一点,过点P作⊙O的切线,切点为C,∠APC的平分线PD与AC交于点D.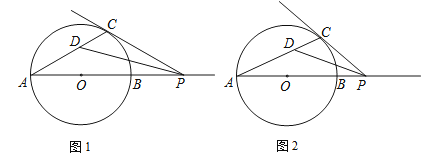
(1)如图1,若∠CPA恰好等于30°,求∠CDP的度数;
(2)如图2,若点P位于(1)中不同的位置,(1)的结论是否仍然成立?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”长假期间,小张和小李决定骑自行车外出旅游,两人相约一早从各自家中出发,已知两家相距10千米,小张出发必过小李家.
(1)若两人同时出发,小张车速为20千米,小李车速为15千米,经过多少小时能相遇?
(2)若小李的车速为10千米,小张提前20分钟出发,两人商定小李出发后半小时二人相遇,则小张的车速应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数有( )
①-a一定是负数;②|-a|一定是正数;③倒数等于它本身的数是±1;
④绝对值等于它本身的数是1;⑤两个有理数的和一定大于其中每一个加数;⑥若![]() ,则a=b.
,则a=b.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com