
【题目】古希腊数学家把数1,3,6,10,15,21,……叫做三角形数,它有一定的规律性,若把第一个三角形数记为a1 ,第二个三角数形记为a 2 ,……,第n个三角形数记为an,计算a2-a1,a 3-a2……由此推算a 100-a 99 =________;a100=________.
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图是8×8的正方形网格,每个小方格都是边长为1的正方形,A、B是格点(网格线的交点).以网格线所在直线为坐标轴,在网格中建立平面直角坐标系xOy,使点A坐标为(﹣2,4).
(1)在网格中,画出这个平面直角坐标系;
(2)在第二象限内的格点上找到一点C,使A、B、C三点组成以AB为底边的等腰三角形,且腰长是无理数,则点C的坐标是 ;并画出△ABC关于y轴对称的△A′B′C′.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,若PA=5cm,C是![]() 上的一个动点(点C与A、B两点不重合),过点C作⊙O的切线,分别交PA、PB于点D、E,求△PED的周长是多少?
上的一个动点(点C与A、B两点不重合),过点C作⊙O的切线,分别交PA、PB于点D、E,求△PED的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,AB=AC=2,点O是边BC的中点,半圆O与△ABC相切于点D、E,则阴影部分的面积等于( )
A.1﹣![]()
B.![]()
C.1﹣![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读完成问题:
数轴上,已知点A、B、C.其中,C为线段AB的中点:
(1)如图,点A表示的数为-1,点B表示的数为3,则线段AB的长为 , C点表示的数为 ;

(2)若点A表示的数为-1,C点表示的数为2,则点B表示的数为 ;
(3)若点A表示的数为t,点B表示的为t+2,则线段AB的长为 ,若C点表示的数为2,则t= ;
(4)点A表示的数为![]() ,点B表示的为
,点B表示的为![]() ,C点位置在-2至3之间(包括边界点),若C点表示的数为
,C点位置在-2至3之间(包括边界点),若C点表示的数为![]() ,则
,则![]() +
+![]() +
+![]() 的最小值为 ,
的最小值为 ,![]() +
+![]() +
+![]() 的最大值为 .
的最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为8cm2,AP垂直∠B的平分线BP于P,则△PBC的面积为( )
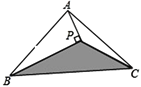
A. 3cm2 B. 4cm2 C. 5cm2 D. 6cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点E.
(1)如图1,若∠ABC=90°,求证:OE∥AC;
(2)如图2,已知AB=AC,若sin∠ADE=![]() , 求tanA的值.
, 求tanA的值.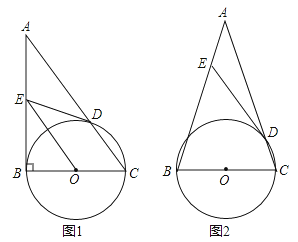
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°.如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处.那么旋转的角度等于( ) 
A.55°
B.60°
C.65°
D.80°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com