
【题目】在一条笔直的公路上有A、B、C三地,A地在B、C两地之间.甲、乙两辆汽车分别从B、C两地同时出发,沿这条公路匀速相向行驶,分别到达目的地C、B两地后停止行驶.甲、乙两车离A地的距离y1、y2(千米)与行驶时间x(时)的函数关系如图所示.
(1)求线段MN的函数表达式;
(2)求点P的坐标,并说明点P的实际意义;
(3)在图中补上乙车从A地行驶到B地的函数图象.

【答案】(1)y=﹣100x+120;(2)点P的坐标为(![]() ,
,![]() ),点P的实际意义表示行驶了
),点P的实际意义表示行驶了![]() 小时后,甲、乙两车相遇,此时离A地的距离为
小时后,甲、乙两车相遇,此时离A地的距离为![]() 千米;(3)见解析.
千米;(3)见解析.
【解析】
(1)根据函数图象中的数据,用待定系数法可以求得线段MN的函数表达式;
(2)根据题意和函数图象中的数据可以求得点P的坐标,并说明点P的实际意义;
(3)根据题意可以求得乙车到达B地的时间,从而可以将图象补充完整.
(1)设线段MN的函数表达式为y=kx+b,
![]()
解得,![]() ,
,
即线段MN的函数表达式为y=﹣100x+120;
(2)∵v甲=80÷1=80,v乙=120÷1.2=100.
∴(120+80)÷(100+80)=![]()
把x=![]() 代入y=﹣100x+120,得y=
代入y=﹣100x+120,得y=![]()
∴点P的坐标为(![]() ,
,![]() ),
),
点P的实际意义表示行驶了![]() 小时后,甲、乙两车相遇,此时离A地的距离为
小时后,甲、乙两车相遇,此时离A地的距离为![]() 千米;
千米;
(3)∵80÷100=0.8,
∴乙车从A地行驶到B地的函数图象如右图所示.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=45°,点D是BC边上一动点(与点B,C不重合),点E与点D关于直线AC对称,连结AE,过点B作BF⊥ED的延长线于点F.
(1)依题意补全图形;
(2)当AE=BD时,用等式表示线段DE与BF之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是8×8的正方形网格,每个小方格都是边长为1的正方形,A、B是格点(网格线的交点).以网格线所在直线为坐标轴,在网格中建立平面直角坐标系xOy,使点A坐标为(﹣2,4).
(1)在网格中,画出这个平面直角坐标系;
(2)在第二象限内的格点上找到一点C,使A、B、C三点组成以AB为底边的等腰三角形,且腰长是无理数,则点C的坐标是 ;并画出△ABC关于y轴对称的△A′B′C′.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某一景点等候检票的时间,随机调查了部分游客,统计了他们进入该景点等候检票的时间,并绘制成如图表.
等候时间x(min) | 频数(人数) | 频率 |
10≤x<20 | 8 | 0.2 |
20≤x<30 | 14 | a |
30≤x<40 | 10 | 0.25 |
40≤x<50 | b | 0.125 |
50≤x<60 | 3 | 0.075 |
合计 | 40 | 1 |
(1)这里采用的调查方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)表中a= ,b= ,并请补全频数分布直方图;
(3)根据上述图表制作扇形统计图,则“40≤x<50”所在扇形的圆心角度数是 °.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB、AC边的垂直平分线分别交BC边于点M、N.
(1)如图①,若△AMN是等边三角形,则∠BAC= °;
(2)如图②,若∠BAC=135°,求证:BM2+CN2=MN2.
(3)如图③,∠ABC的平分线BP和AC边的垂直平分线相交于点P,过点P作PH垂直BA的延长线于点H.若AB=4,CB=10,求AH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A、B),过点P作半圆O的切线分别交过A、B两点的切线于D、C,连接OC、BP,过点O作OM∥CD分别交BC与BP于点M、N.下列结论:
①S四边形ABCD= ![]() ABCD;
ABCD;
②AD=AB;
③AD=ON;
④AB为过O、C、D三点的圆的切线.
其中正确的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,若PA=5cm,C是![]() 上的一个动点(点C与A、B两点不重合),过点C作⊙O的切线,分别交PA、PB于点D、E,求△PED的周长是多少?
上的一个动点(点C与A、B两点不重合),过点C作⊙O的切线,分别交PA、PB于点D、E,求△PED的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点E.
(1)如图1,若∠ABC=90°,求证:OE∥AC;
(2)如图2,已知AB=AC,若sin∠ADE=![]() , 求tanA的值.
, 求tanA的值.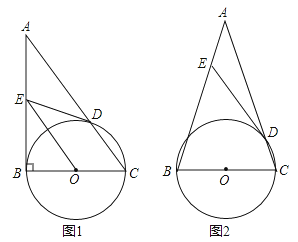
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com