
【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8;乙:9,6,10,8,7;
![]() 将下表填写完整:
将下表填写完整:
平均数 | 中位数 | 方差 | |
甲 | ______ | 8 | ______ |
乙 | 8 | ______ | 2 |
![]() 根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
![]() 若乙再射击一次,命中8环,则乙这六次射击成绩的方差会______
若乙再射击一次,命中8环,则乙这六次射击成绩的方差会______![]() 填“变大”或“变小”或“不变”
填“变大”或“变小”或“不变”![]()
【答案】8;0.4;8;变小
【解析】分析:(1)依据平均数、中位数依据方差的计算方法进行计算;
(2)依据甲的成绩较稳定,即可得到结论;
(3)求得乙这六次射击成绩的方差,即可得到变化情况.
详解:(1)甲平均数为(8+7+9+8+8)÷5=8,
甲的方差为:![]() [(8-8)2+(7-8)2+(9-8)2+(8-8)2+(8-8)2]=0.4,
[(8-8)2+(7-8)2+(9-8)2+(8-8)2+(8-8)2]=0.4,
乙的环数排序后为:6,7,8,9,10,故中位数为8;
故答案为:8,0.4,8;
(2)选择甲.理由是甲的成绩较稳定.
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差为:![]() [(9-8)2+(6-8)2+(10-8)2+(8-8)2+(7-8)2+(8-8)2]=
[(9-8)2+(6-8)2+(10-8)2+(8-8)2+(7-8)2+(8-8)2]=![]() <2,
<2,
∴方差会变小.
故答案为:变小.


科目:初中数学 来源: 题型:
【题目】在数轴上,点A,B,C表示的数分别是-6,10,12.点A以每秒3个单位长度的速度向右运动,同时线段BC以每秒1个单位长度的速度也向右运动.
(1)运动前线段AB的长度为________;
(2)当运动时间为多长时,点A和线段BC的中点重合?
(3)试探究是否存在运动到某一时刻,线段AB=![]() AC?若存在,求出所有符合条件的点A表示的数;若不存在,请说明理由.
AC?若存在,求出所有符合条件的点A表示的数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E,F是对角线AC上的两点且AE=CF,在①BE=DF;②BE∥DF;③AB=DE;④四边形EBFD为平行四边形;⑤S△ADE=S△ABE;⑥AF=CE这些结论中正确的是_____.
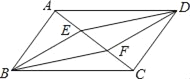
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P为四边形ABCD边上的任意一点,当∠BPC=30°时,CP的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题: 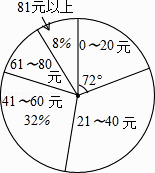
捐款 | 人数 |
0~20元 | |
21~40元 | |
41~60元 | |
61~80元 | 6 |
81元以上 | 4 |
(1)全班有多少人捐款?
(2)如果捐款0~20元的人数在扇形统计图中所占的圆心角为72°,那么捐款21~40元的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N. 
(1)求证:OM=AN;
(2)若⊙O的半径R=3,PA=9,求OM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的对称轴为经过点(1,0)的直线,其图象与x轴交于点A、B,且过点C(0,﹣3),其顶点为D.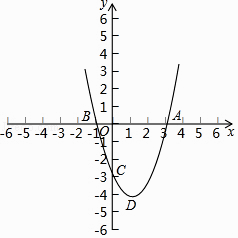
(1)求这个二次函数的解析式及顶点坐标;
(2)在y轴上找一点P(点P与点C不重合),使得∠APD=90°,求点P的坐标;
(3)在(2)的条件下,将△APD沿直线AD翻折得到△AQD,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?

(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题: 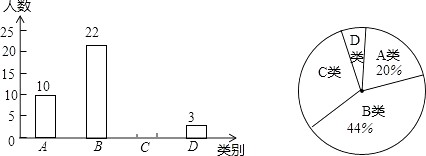
(1)本次抽取样本容量为 , 扇形统计图中A类所对的圆心角是度;
(2)请补全条形统计图;
(3)若该校九年级男生有600名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com