
【题目】如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N. 
(1)求证:OM=AN;
(2)若⊙O的半径R=3,PA=9,求OM的长.
【答案】
(1)证明:如图,连接OA,则OA⊥AP,

∵MN⊥AP,
∴MN∥OA,
∵OM∥AP,
∴四边形ANMO是矩形,
∴OM=AN;
(2)解:连接OB,则OB⊥BP

∵OA=MN,OA=OB,OM∥AP.
∴OB=MN,∠OMB=∠NPM.
∴Rt△OBM≌Rt△MNP,
∴OM=MP.
设OM=x,则NP=9﹣x,
在Rt△MNP中,有x2=32+(9﹣x)2
∴x=5,即OM=5.
【解析】(1)连接OA,由切线的性质可知OA⊥AP,再由MN⊥AP可知四边形ANMO是矩形,故可得出结论;(2)连接OB,则OB⊥BP由OA=MN,OA=OB,OM∥AP.可知OB=MN,∠OMB=∠NPM.故可得出Rt△OBM≌△MNP,OM=MP. 设OM=x,则NP=9﹣x,在Rt△MNP利用勾股定理即可求出x的值,进而得出结论.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】 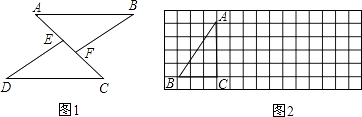
(1)如图1,点E、F在AC上,AB∥CD,AB=CD,AE=CF,求证:△ABF≌△CDE
(2)如图2,方格纸中的每个小方格是边长为1个单位长度的正方形. ①画出将Rt△ABC向右平移5个单位长度后的Rt△A1B1C1
②再将Rt△A1B1C1绕点C1顺时针旋转90°,画出旋转后的Rt△A2B2C2 , 并求出旋转过程中线段A1C1所扫过的面积(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.
(1)证明:AD垂直平分CE;
(2)若∠BCE=40°,求∠EHD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C是AB的中点,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为x秒(x>0).
(1)当x= 秒时,点P到达点A;
(2)运动过程中点P表示的数是 (用含x的代数式表示);
(3)当P,C之间的距离为2个单位长度时,求x的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8;乙:9,6,10,8,7;
![]() 将下表填写完整:
将下表填写完整:
平均数 | 中位数 | 方差 | |
甲 | ______ | 8 | ______ |
乙 | 8 | ______ | 2 |
![]() 根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
![]() 若乙再射击一次,命中8环,则乙这六次射击成绩的方差会______
若乙再射击一次,命中8环,则乙这六次射击成绩的方差会______![]() 填“变大”或“变小”或“不变”
填“变大”或“变小”或“不变”![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆统景温泉风景区被喻为“巴渝十二景”.为丰富旅游配套资源,镇政府决定大力发动农户扩大柑橘和蔬菜种植面积,并取得了较好的经济效益.今年该镇柑橘和蔬菜的收成比去年增加了80吨,其中柑橘的收成比去年增加了20%,蔬菜的收成比去年增加了30%,从而使今年的收成共达到了420吨.
(1)统景镇去年柑橘和蔬菜的收成各是多少吨?
(2)由于今年大丰收,镇政府计划用甲、乙两种货车共33辆将柑橘和蔬菜一次性运去参加渝洽会.已知一辆甲种货车最多可装13吨柑橘和3吨蔬菜;一辆乙种货车最多可装柑橘5吨和蔬菜6吨,安排甲、乙两种货车共有几种方案?
(3)若甲种货车的运费为每辆600元,乙种货车的运费为每辆500元,在(2)的情况下,如何安排运费最少,最少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则△A′B′C的周长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班准备购买大课间活动器材呼啦圈和跳绳,已知购买1根跳绳和2个呼啦圈要35元,购买2根跳绳和1个呼啦圈要25元.
(1)求每根跳绳、每个呼啦圈各多少元?
(2)根据班级实际情况,需购买跳绳和呼啦圈的总数量为30,总费用不超过300元,但不低于280元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com